Kjenn dine akser!

Kjennskap til og forståelse for dimensjonene vår eksistens er begrenset til gjør at vi kan utnytte dem til vår fordel.

Vi lever i en 3-dimensjonal verden. Så langt i hvert fall.

Vi kan bevise det ved å tegne en strek, for så å strekke en ny strek fra den som er 90° i forhold til den første, på samme plan.

Dette kan vi gjøre én gang til, men den kan ikke være på det samme planet! Den nye streken er nå 90° på de to andre strekene.

Nå har vi 3 streker som peker hver sin retning. Kan vi gjøre det igjen? Nei, det går ikke, det er ikke flere dimensjoner å strekke seg ut i som gjør at en fjerde strek vil være 90° i forhold til alle de andre strekene.

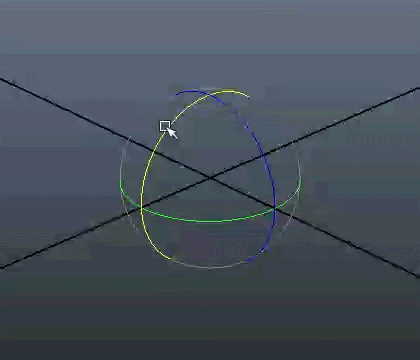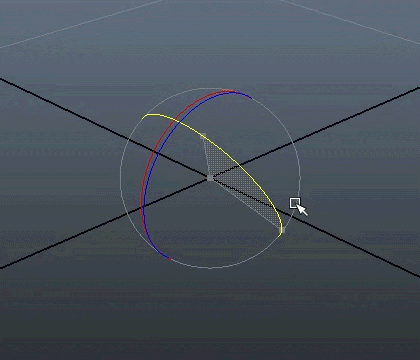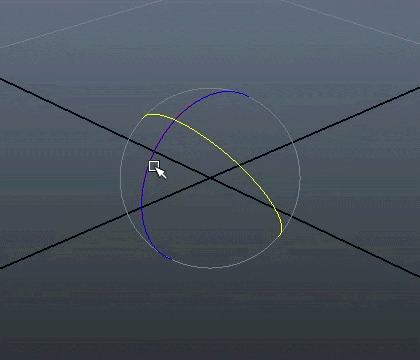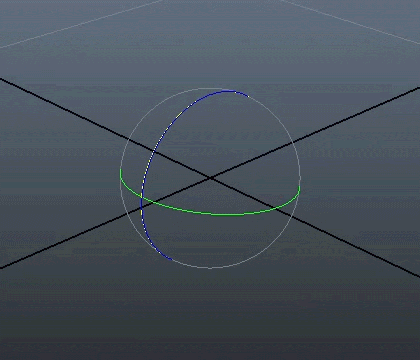
Under er en visuell representasjon av dimensjonene. Legg merke til at selv om bildet vises på en 2D skjerm, kan vi fremdeles simulere 3 dimensjoner, som gir bildet perspektiv.

Men kanskje den ikke trenger å være det i den fjerde dimensjonen, hva vet jeg, men i de tre dimensjonene vi lever i går det i hvert fall ikke an.

En roterende hyperkube. Et forsøk på å visualisere en 4-dimensjonal kube, kjent som en tesserakt. Det ser ikke sånn ut, men alle vinklene er teoretisk sett 90°.

---

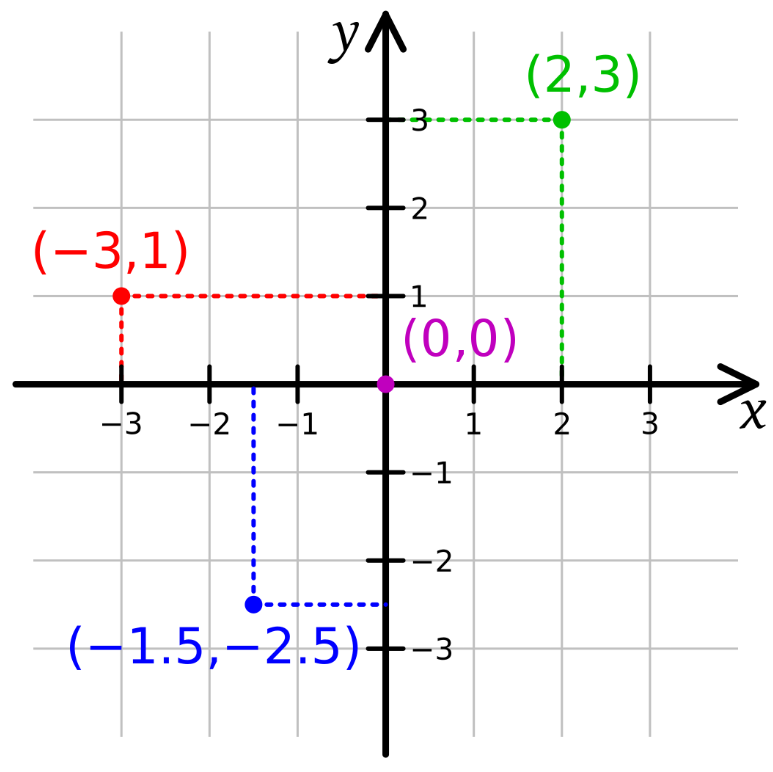
Kartesisk koordinatsystem

Et punkt på et plan er definert med et koordinat. Ordet koordinat er for øvrig et sammensatt ord av prefikset ko-, som betyr sammen eller til, og baseordet ordinat, som kommer fra Latin ordinare, og betyr å ordne eller sette i rekkefølge. Et ordinat er et punkt på samme linje parallelt med en akse, vanligvis Y-aksen i matematikk, og ordinater langs X-aksen kalles for en abscisse. Disse to verdiene… koordinerer… med hverandre for å definere et punkt på et plan. Dette er et koordinat.

Aksene som utgjør et koordinatsystem kalles X og Y, der X alltid er den horisontale og Y alltid er den vertikale.

Koordinater defineres med variablene X og Y i parentes slik: (X, Y) som definerer en distanse langs den respektive aksen fra nullpunktet i midten der aksene krysser. Dette punktet heter origo, fra Latin opphav eller opprinnelse. Variablene oppgis ALLTID i alfabetisk rekkefølge. (Den fjerde dimensjonen oppgis faktisk med W, men det er fordi det ikke er flere bokstaver etter Z i det engelske alfabetet. Kanskje vi burde kalle den Æ-aksen her til lands. Det angår uansett ikke oss, så nok om det.)

Et koordinatsystem er delt inn i 4 kvadranter. Ordet kvadrant kommer fra Latin quad, som betyr fire, eller fjerde, og derav quadrans som betyr en kvart. Det er vanlig å operere i den første kvadranten i et koordinatsystem. Første kvadrant er alltid opp og til høyre. Deretter går de mot klokken. Alle koordinater i første kvadrant er positive i forhold til origo.

Et punkt i rom er definert med 3 verdier. X, Y og Z. Men hvor går Z-aksen? Åpenbart perpendikulært til X og Y, men det kommer selvsagt an på referansebildet og hvor du ser det fra.

Et koordinatsystem kan enten være spesifisert ut fra et globalt referansepunkt, eller et lokalt referansepunkt. Et globalt referansepunkt vil si et koordinatsystem som er overordnet alle andre systemer i det. Et objekt i et globalt koordinatsystem kan ha en posisjon, rotasjon eller vinkling som gjør at dets lokale koordinatsystem er helt annerledes orientert enn det globale, men dets posisjon og rotasjon kan defineres innen det globale systemet det befinner seg i.

I et koordinatsystem med 3 akser er det 8 seksjoner. Disse kalles oktanter. Jeg trenger nok ikke forklare hvor det ordet kommer fra.

Hvis man ser nøye etter på bildet over, så ser vi at Z-aksen ligger ned og Y-aksen går vertikalt. Dette er for så vidt helt legitimt, men presenterer et unikt problem. Hvordan det koordinatsystemet vi bruker er orientert i det ultimate globale systemet alle koordinatsystemer er underlagt; virkeligheten.

Akkurat dette problemet med hvilken retning Z skal gå er noe som har plaget meg i lengre tid. Det virker som det er et problem som avhenger av hvordan du velger å se på det. Et problem som muligens har sine røtter i klasserommet når man først lærer om koordinatsystemer.
Se for deg at du har tegnet et 2-dimensjonalt koordinatsystem på et ark på et bord, liggende flatt på bordet som om du var eleven som skrev det i rutearkboken din; hvis du nå skulle legge til Z-aksen, hvilken retning ville den gått? Oppover, ikke sant? Opp fra bordflaten? Mot himmelen?
Eller gir det mer mening å se på tavlen til læreren, eller løfte opp boken, slik at Y-aksen nå peker oppover og Z-aksen nå kommer ut mot deg som på bildet over?

Jeg har alltid tenkt på det som det første eksempelet. At Z går oppover, gir rommet høyde, i motsetning til utover og gir rommet dybde.
Hvis du tenker deg rutenettet som jorden er delt opp i, altså lengdegrader og breddegrader, X og Y, så kan elevasjonen (altituden) , Z, kun gå én vei, opp.

---

I praksis

Sannheten er at begge måter å se på det er korrekt, men det er viktig å ha i tankene. Når vi beveger oss inn i praktisk bruk av koordinatsystemer, spesielt i maskiner, er det særdeles viktig å holde tunga rett i munnen og vite hvilken orientering maskinens koordinatsystem har, for å kunne korrekt forutsi maskinens bevegelser.

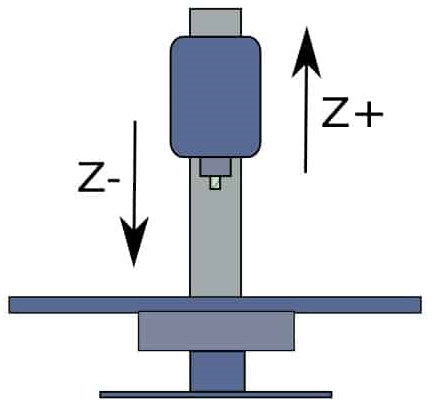
Heldigvis har vi flere tommelfingerregler for å hjelpe oss. Den første og viktigste er denne: Z er alltid spindelaksen!

Venstre: Vertikal fresemaskin. Høyre: Horisontal fresemaskin.

Regel nummer to er at alle bevegelser forekommer i forhold til spindelen.

For selve spindelaksen er Z+ alltid vekk fra arbeidsstykket.

På maskinen over er det bordet som beveger seg, mens spindelen står stille. Dette er ganske vanlig, men det er allikevel spindelen som er referansepunktet i maskinen. Alle bevegelser går i forhold til spindelen. På bildet over ser vi en ganske normal, universal vertikal fres. Pilene definerer aksenes positive og negative retninger i forhold til spindelen. Hvis vi skal bevege verktøyet til et positivt X-koordinat, vil bordet bevege seg mot venstre. Det samme gjelder Y. Hvis vi skal til f.eks. et negativt Y-koordinat, vil bordet bevege seg innover. Pilene på bildet over definerer retningene i forhold til spindelen. Hadde spindelen beveget seg hadde de vært “korrekt“, men siden den står stille og bordet beveger seg, blir det bevegelser omvendt for at bevegelsene skal bli korrekt i forhold til spindelen.

På maskiner hvor det ikke nødvendigvis er umiddelbart klart hvilken akse som er hvem og hvilken retning som er positiv, kan vi bruke en kjekk huskeregel:

---

Høyrehåndsregelen

Ved å holde hånden som på bildet over, og peke langfingeren langs spindelaksen, kan vi raskt og enkelt finne aksene i maskinen.

Denne regelen er så elementær i både matematikk, fysikk og mekanikk, at den til å med figurerer på Sveitsiske 200 Franc-sedler:

Kjent i Sveits som règle de la main droite på Fransk, eller Right Hand Rule på engelsk i resten av verden.

Kanskje mer kjent fra elektrisitetens verden, der den ofte brukes til å huske retningen på magnetiske felt og slikt, men den er like nyttig for oss som trenger den for å forme metall til vår vilje.

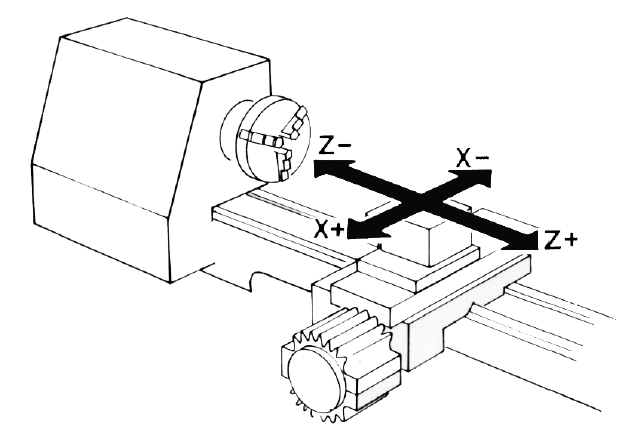
I dreiebenker er det litt annerledes siden det er arbeidsstykket som står i spindelen og verktøyet som står stille, men det er fremdeles spindelen som er primus motor når vi skal referere koordinatsystemet og aksene i en dreiebenk.

For at dette skal gi mening med håndregelen må vi faktisk benytte venstrehåndsregelen. Vi må også holde den opp som om vi peker pekefingeren mot taket.
Men det kommer selvsagt an på hva slags dreiebenk man jobber med, eller hvilken side av arbeidsstykket sleiden/verktøyet er montert.
Minus-retningen er alltid nærmere arbeidsstykket.

Dessverre er det slik at ikke alle maskinfabrikanter håndhever (get it?) disse “reglene“ og de stemmer ikke alltid. Men stort sett er de korrekt. Det er korrekt når de er korrekt.

---

Akseplan

Når to akser elsker hverandre veldig mye, former de et akseplan. Et plan er et to-dimensjonalt objekt og krever to retninger for å definere.

Siden det er 3 akser finnes det 3 primære akseplan.

Planene defineres med de to aksene som utgjør definisjonen av planet.
XY-planet er det horisontale planet, mens XZ og YZ planene er vertikale i hver sin retning.

---

Rotasjon

Akkurat som vi kan bevege oss langs aksene, kan vi i tredimensjonalt rom også bevege oss rundt dem. Hver akse representerer en mulighet for rotering rundt den, låst fast til den. Disse rotasjonsretningene kalles også akser; rotasjonsakser.

De er definert med bokstavene A, B og C, der de følger logisk alfabetisk rekkefølge og relasjon til X, Y og Z:

A er rotasjon rundt X.
B er rotasjon rundt Y.
C er rotasjon rundt Z.

Men hvilken rotasjonsretning er positiv?

Det må naturligvis defineres i relasjon til aksen den dreier om sin positive retning.

På samme måte som jorden, hvis du ser ned på den fra nordpolen dreier den mot klokka. Dette er korrekt for rotasjonsaksene også.

Ser man ned langs dem fra deres positive retning vil pluss-rotasjon være mot klokken.

Det finnes heldigvis en enklere måte å huske dette på, og igjen kommer vår gode venn høyrehåndsregelen til unnsetning igjen:

Hvis du former høyrehånden som om du skal signalisere tommel opp, og peker tommelen langs aksens positive retning, vil de resterende fingrenes pekeretning indikere positiv rotasjon.

---

Representasjon av aksene

I CAD-programmer og 3D-programmer heter den lille klumpen med 3 piler i hver sin retning en “triad”.
Den vises vanligvis i et hjørne på skjermen og brukes til orientering av skjermbildet. Tenk på den som et kompass.

Den oppstår også ofte på et punkt hvis du trykker på det, eller prøver å flytte noe.
Der brukes de hovedsakelig til å translatere (bevege lineært) og rotere - og i noen tilfeller - skalere.
Noen ganger vises de med akseplan, og tar man tak i de kan delen flyttes på planet.

Grunnen til at det kalles en “triad” er fordi den representerer et hjørne på en kube, og en triade er en av 3 (13) mulige symmetriakser i en kube:

Apropos ingenting: på engelsk heter en akse for axis, og flertallet er axes, uttalt med lang e, axees.

Du har sikkert sett triader før eller representasjoner av tre akser der aksene har hver sin farge. Du har sikkert også lagt merke til at de ofte varierer på hvilken farge som representerer hvilken akse?

Vel, det er én korrekt måte å farge aksene på, og det er igjen i logisk alfabetisk rekkefølge basert på de tre lys-additive primærfargene, Rød, Grønn og Blå.

X er Rød.
Y er Grønn.
Z er Blå.

Så sånn er det med den saken.

---

Euler-angles og Gimbal-lock

Rotasjon rundt primæraksene defineres i grader, og når disse 3 gradsystemene kombineres kalles de for “Euler-angles”, etter igjen, den legendariske Leonhard Euler.

En hvilken som helst vinkling og akse-rotasjon kan nåes innen 3 bevegelser.

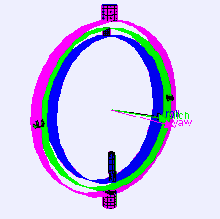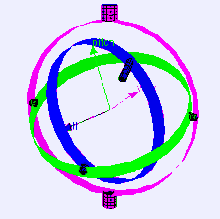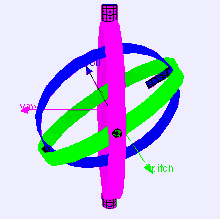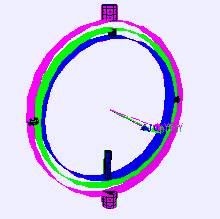
Dette systemet visualiseres ofte med noe som kalles en “gimbal”. Tenk på det som en triade spesifikt for rotasjon.

Dersom du vrir en akse 90 grader slik at rotasjon rundt den nå koinsiderer med rotasjon rundt en annen akse, har vi oppnådd noe som kalles for “gimbal-lock“.

Med gimbal-lock mister man en rotasjonsakse og kan ikke lenger oppnå visse posisjoner/rotasjoner.

Men dette problemet angår ikke oss så veldig, men det er kjekt å ha i bakhodet. Det er et større problem i animasjon og 3D-grafikk, men nå har de noe som heter quaternions, som navnet tilsier bruker 4 verdier for å beskrive en vinkel og rotasjon, men det skal jeg ikke gå inn på fordi det er ikke relevant for dette innlegget og det er svart magi jeg ikke forstår meg på.

---

Magien av 5 akser

Dersom vi har en maskin med rotasjon rundt 2 akser, har vi totalt 5 bevegelige akser, og kan gjøre 5-akse maskinering. I slike maskiner er det vanlig å ha rotasjon rundt X og Z, altså A og C, men siden rotasjon rundt Y ikke er tilgjengelig eller relevant (man kan oppnå det ved å tilte A 90°), blir aksene ofte kalt A og B, spesielt i maskiner der bordet beveger seg og ikke spindelhodet, eller der rotasjonsaksene er lagt til senere eller på annet vis ikke integrale i maskinens design. Dette har flere årsaker, som å poengtere at aksene det dreier seg om er for bevegelse av arbeidsstykket eller bordet, og fordi C-aksen vanligvis definerer spindelaksen, og hvis man vrir A er ikke C lenger koaksial med Z.

Viktig notat: I en bordbasert 5-akse maskin er nullpunktet alltid der A-aksen og C-aksen (B), møtes.

Dessuten har ikke “C“ aksen noe formål i maskiner der man kan oppnå det samme resultatet med XY interpolering, men dersom man vrir A 90° slik at “C“ aksen nå er på linje med Y-aksen vil den ha et formål, og den fungere da teknisk sett som en B-akse.

En måte å tenke på det på er at med bordet i normalposisjon er B-asken gimbal-locked til C-aksen. Ved å vri A-aksen har vi nå tilgang til alle vinkler.

Under er to forskjellige eksempler på ulike 5-akse maskiner.

Bordbasert Maskin med A- og B-akse

Spindelbasert Maskin med A- og C-akse

Håper du nå er litt mer kjent med aksene vi forholder oss til på en daglig basis! Husk: Uansett hvilket koordinatsystem du befinner deg i, så lenge du er klar over det, med XYZ-ABC-RGB og høyrehåndsregelen så kan du aldri gå feil!

Alt du trenger å vite om: Borehode

Et borehode, også kalt utboringshode, (eng.: boring head) er en meget nyttig, nesten uunnværlig, innretning og tilleggsutstyr til enhver vertikal fres.

Et borehode med tilhørende verktøysett.

I all hovedsak er det en måte å transformere en fres om til en “omvendt dreiebenk”, i den forstand at det gjør maskinen i stand til å lage sirkulære former, men arbeidsstykket står fortsatt stille mens verktøyet beveger seg. Forskjellen er at verktøyet som benyttes er en ‘single point cutter‘, vanligvis i form av en borestang (eng.: boring bar).

Et verktøy som i utgangspunktet er beregnet til innvendig dreiing er ypperlig for bruk i et borehode siden det vanligvis har to viktige egenskaper; stor endeklaring og høy spissvinkel. Med andre ord er det formet slik at det presenterer kuttpunktet sitt ut og vekk fra kroppen. Når det kommer til borestenger beregnet for bruk i borehoder er det ikke uvanlig at de har null endeklaring, d.v.s. at de er flate i bunnen, som ofte kan være en fordel.

Borehoder er ypperlig for å lage store hull som må ha en eksakt dimensjon (innvendig boring), forstørre eksisterende hull, forbedre overflatefinheten på hull og lignende. Når man bruker et borehode er det vanlig å finne senter av operasjonen som skal utføres, for så å låse X og Y aksene og mate i Z. Avhengig av operasjonen er det mulig å bruke spindelmating, men det er anbefalt å flytte Z-aksen i steden, for økt stivhet og resultat.

Det kan også brukes til det motsatte, å lage sirkulære protruderende aksler (utvendig boring), som ellers ikke ville vært mulig å lage uten et rundmatingsbord eller sirkulær interpolering på en CNC-maskin.

Her stilles verktøyet til riktig diameter og mates nedover, på samme måte som innvendig boring, men - avhenging av verktøyet - må spindelrotasjonen snus, som om vi dreier på “baksiden“ av kjoksen i en dreiebenk.

Typiske operasjoner for borehoder:

Et borehode har et par deler hvis funksjon ikke nødvendigvis er videre opplagt. Kunnskap om disse er nødvendig for flere av operasjonene over. Borehoder kommer i ulike grader av kompleksitet.

De er essensielt delt opp i to deler: snekkehuset (kroppen) og sleiden (eng.: body & slide). De er festet sammen med et svalehalespor (eng.: dovetail) og en justeringsskrue som endrer diameteren på kuttet.

Hovedskruen (eng.: quick setting spindle) er hovedsakelig en grovinnstilling og brukes til å endre diameter raskt. En omdreining her flytter vanligvis sleiden flere millimeter av gangen. Finjustering gjøres med snekkeskruen på siden som er delt opp i hundredels millimetere. Normalt sett er denne oppgitt for diameteren på arbeidsstykket, ikke bevegelsen av sleiden, slik at hvis man flytter skruen én gradering øker man diameteren med 0,01mm, med andre ord flytter sleiden seg 0,005mm. Dette er oppgitt på hodet. Pilene indikerer hvilken retning som flytter sleiden en spesifikk vei.

Bildet over er av et mer avansert borehode, ofte kalt et automatisk borehode eller universalt borehode (eng.: universal boring head, facing & boring head). Det har den funksjonen at det kan mates radialt mens verktøyet roterer, slik at man kan plane eller lage radiale spor i bunnen eller andre steder langsmed hullet eller akselen.

Her ser vi snekkeskruen for finjustering (eng.: fine setting spindle, worm with scale), låseskruen som låser sleiden (eng.: clamping screw, arrest screw), strammeskruer for gib’en (en bit som ligger mellom de to delene i svalehalesporet for å justere slarken, jeg vet ikke om den har noe godt norsk navn) (eng.: slide tension, gib adjust screw), og strammeskruene for å feste verktøyet. Verktøyhullene er vanligvis Ø16 H7.

Det er viktig at verktøyet peker i den retningen man planlegger å mate sleiden, med kuttepunktet/kuttesiden så parallell som mulig med sleiden. Et par grader fra eller til spiller liten rolle, men et stort avvik vil endre både kutteferdighetene, og overenstemmelsen mellom justeringsskrue og faktisk mål.

Hovedskruen og gib’en, samt verktøyhullet i siden som gjør det mulig å montere verktøy stikkende rett ut for maksimal rekkevidde.

Over ser vi baksiden der vi finner de to endestoppene (eng.: feed dogs, stops), som avbryter automatisk radiell mating, og kan stilles etter ønsket diameter. En for hver vei. I midten finner vi utløseren (eng.: fixed pin) som endestoppene treffer slik at motstanden blir så stor at clutchen løser ut. Det er en oljenippel på hver side for å smøre sleiden.

Nå kommer vi til hjertet av det universale borehodet:

For å aktivere radiell mating må clutchpinnen presses ned i clutchsporet, slik at den aktiveres. Dette kan gjøres med en flat skrutrekker eller lignende. Ringen som pinnen sitter i (eng.: holding ring) roterer fritt. Under sitter materingen (eng.: scale ring) med et spor som clutchpinnen rir i når matingen er aktivert. Denne er koblet til finjusteringsskruen.

Materingen har vanligvis et par ulike valg for matehastigheter, under ser vi 0, 2, 4 og 6, som representerer hundredels millimetere økning i diamater per revolusjon. Her er borehodet stilt inn til 0,06mm/rev mating. 0 betyr at borehodet ikke vil mate, selv om clutchen er lagt inn. Matehastigehten stilles inn ved å vri på matejustering-ringen med det røde indikasjonmerket.

I clutchringen er det en settskrue som justerer clutchstyrken, altså hvor mye last som skal til før clutchen utløser og stopper matingen. Den har også et hull for håndtak som man er nødt til enten å holde selv eller hvile inntil en stasjonær del av maskinen. Når spindelen igangsettes og håndtaket holdes igjen vil de tre ringene stå stille mens resten av hodet roterer og mater utover til man slipper håndtaket, eller; til endestoppen treffes eller verktøyet overbelastes, begge ting som vil belaste clutchen slik at den løser ut.

Enda mer feinschmecker borehoder som også kan mate aksialt, og begge to samtidig (slik at man kan bore koner!) eksisterer fra produsenter som f.eks. Wohlhaupter.

Ingen borehoder kommer med skala, så vidt jeg vet. Det eksisterer digitale borehoder som gir deg enkel avlesning av diameter, men disse er ikke til bruk i manuelle maskiner, stort sett.

Så, hvordan setter man borehodet til å kutte riktig diameter?

Det er hovedsakelig to måter å finne dimensjonene sine:

Den første og enkleste er rett og slett å ta et kutt og måle, for så å justere videre derfra.

Den andre er som følger:

1. Finn en kant på arbeidstykket, eller på et stykke offermateriale

2. Sett spindel-senter på denne kanten

3. Null avlesningen på fresen

4. Flytt kanten bort fra senter lik radien til ønsket kutt

5. Juster borehodet til verktøyet berører kanten

6. Et voilá!

På bildet helt øverst i innlegget er det avbildet et borehode med litt tilleggsutstyr. Dette kan kombineres for å utføre en rekke oppgaver:

Og hvis man føler seg riktig freidig kan man kombinere verktøy som f.eks slik:

Borehoder bør ikke kjøres over 1000 RPM, spesielt ikke hvis sleiden er skrudd langt til en side. Dette kan skape vibrasjoner som gir dårligere nøyaktighet og finish. Større hoder bør ikke kjøres over 600. Når det er sagt, her er noen anbefalte skjæredata:

Men ta dette som EKSTREMT veiledende, og ikke som en fasit! Utover det gjelder skjærehastigheter som ellers for materiale og verktøygrad.

Kuttdybde bør ikke overstige 4mm med en mating på 0,06mm/rev (hverken aksialt eller radialt). Men dette avhenger voldsomt av utstikk, materiale, oppspenning, applikasjon, o.s.v. Som en tommelfingerregel kan kuttdybde økes når mating senkes. Det viktige er at lasten blir lik.

Dersom verktøyet vibrerer (sperrer) anbefales det å senke skjærehastigheten eller øke matingen.

Det er hensiktsmessig å ikke ta for tynne kutt hvis det kan unngås (med mindre det er et finkutt selvsagt). Dersom det benyttes skjær med høy spissvinkel kan en kuttdybde som er større enn neseradien bidra til å stabilisere verktøyet.

Pinnefresens anatomi og hvordan velge riktig verktøy til jobben

Pinnefreser (End Mill) er den vanligste formen for skjæreverktøy til universale freser og valg av riktig pinnefres til jobben som skal gjøres kan utgjøre en stor forskjell. Det er mange dimensjoner å ta hensyn til ved innkjøp og bruk av pinnefreser.

View fullsize

Både materiale som skal freses og applikasjonen er kritiske i valg av fres. 

Kuttdiameter og kuttlengde

Fresens diameter og kuttlengde er åpenbart en vesentlig del å ta hensyn til ved valg av fres. Tykkere freser tåler mer og er mer stabile. Rigiditet og motstand mot vibrasjoner og defleksjon er viktig når det kommer til fresing og derfor bør man bruke så tykk fres som det lar seg gjøre. 

View fullsize

Kuttdiameteren er diameteren på den teoretiske sirkelen som dannes når verktøyet spinner rundt. Dersom fresen ikke står sentrert vil kuttdiameteren øke og fresen vil hovedsakelig skjære på én tann, hvilket er langt fra ideelt.

Total lengde (Overall Length), flutelengde (Length Of Flute) og kuttlengde (Length Of Cut) er kritiske ved bruk av lange freser. Dersom en lang fres må benyttes er det bedre å bruke en med lang hals (lang LBS, Length Below Shaft) og kortere kuttlengde siden den har tykkere kjerne/aksel over en større del av den totale lengden enn en tilsvarende lang fres med lengre kuttlengde:

View fullsize

Akseldiameteren har også betydning for hva slags collet eller annen montering og oppspenning som må benyttes. Ofte er akselen tykkere enn kuttdiameteren slik at det kan være problematisk å komme til dersom man skal frese dype spor eller lignende.

Fluter

Antall fluter spiller en stor rolle for fresens materialfjerningsevne, matehastigheter, sponevakuering, stabilitet og defleksjon. En fres med flere fluter har en tykkere kjerne som gjør den bedre i stand til å stå i mot radiale krefter og kan derfor f.eks. ta dypere/lengre kutt (stikke lenger ned i arbeidsstykket).

View fullsize

Men med mange fluter blir hver flute liten, altså er det liten plass til sponet som produseres ved fresingen. 

View fullsize

Tradisjonelt kom pinnefreser i utforminger med 2 og 4 fluter, der tommelregelen var å bruke 2 fluter på bløte metaller som aluminium, kobber, etc. og 4 fluter på hardere materialer som stål og andre harde legeringer. Grunnen til dette er at bløte metaller som aluminium er lettere å maskinere, samt at de har en tendens til å pakke seg i flutene og hindre sponevakuering dersom flutene blir for små, mens stål og lignende stor sett krever sterkere freser og lager mindre og mer håndterlig spon som lettere lar seg evakuere selv med grunne fluter.

View fullsize

Med flere fluter kan man også benytte høyere matehastigheter eller oppnå finere overflate med samme matehastighet ved å øke antallet fluter. I moderne produksjon der det settes fokus på hurtig maskinering er flere fluter blitt populært fordi det gir sterkere freser som kan mates fortere og fjerne mer materiale samtidig som det forlenger levetiden til verktøyet grunnet lavere stress på hver tann/flute.

View fullsize

View fullsize

Mer fres gir plass til mindre fluter.

Med nyere materialforskning og produksjon er det blitt vanlig med 3 fluter for aluminium fordi det gir en god balanse mellom god sponevakuering og høye matehastigheter.

Endeutforming og profil

Endeutformingen er viktig med tanke på bruken og hvordan fresen skal bevege seg, spesielt med tanke på CNC maskiner.

View fullsize

Blant "normale" pinnefreser finnes det hovedsakelig 4 typer:

• Flat / "vanlig" pinnefres (Square / Flat Nose)
• Avrundet / Radius (Radius Corner / Bull Nose)
• Kule (Ball Nose)
• Fas eller formfres (Chamfer / Formed End)

View fullsize

View fullsize

Avrundede freser, eller radiefreser, er populære der det f.eks. ikke er kritisk med 90° skarpe innvendige hjørner og brukes mye til generell grovforming. Den avrundede kanten på eggen gir en jevnere trykkfordeling på den ellers skarpe tuppen av skjærene som gjør at verktøyet tåler mer og varer lengre. 

Kulefreser er på sett og vis også radiefreser, men de ender ikke opp i en flat del, de lager halvkuler. Disse er mye brukt til forming av kompliserte deler i 3-,4- og 5-akse CNC maskiner der myke overganger mellom passeringer er nødvendig eller rett og slett der det trengs en kanal eller innvendig form med en radius.

Fasefreser eller andre formfreser brukes gjerne til avsluttende passeringer for å fase kanter eller påføre spesielle former på deler av arbeidsstykket.

Når det gjelder flate pinnefreser finnes det hovedsakelig 2 typer: senterskjærende og ikke-senterskjærende

View fullsize

Forskjellen sier seg selv; den ene typen skjærer i midten og kan "plunge", altså stikkes rett ned i arbeidsstykket på samme måte som et bor, den andre kan ikke og må beveges i X eller Y for å skjære.

View fullsize

En annen litt interessant egenskap ved moderne pinnefreser er at tennene mot formodning ikke står helt symmetrisk, men er ofte slipt inn med små variasjoner i gradene mellom dem:

View fullsize

I eksempelet over er det avbildet en 4-fluters flat pinnefres som man skulle tro hadde tenner med 90° intervaller, men de er litt forskjøvet frem eller tilbake slik at ingen av tennene har lik vinkel mellom seg, men vinklene blir selvsagt fortsatt 360° totalt. Dette er for å forhindre "chatter" eller vibrering i verktøyet eller arbeidsstykket ved at fresen treffer en frekvens som resonnerer med intervallene på tennene. Så disse er litt forskjøvet for å forhindre dette.

Heliksvinkel

Heliksvinkelen er den aksiale vinkelen på flutene som går rundt akselen. Vinkelen måles mellom senterlinjen til fresen og en rett linje som går tangentielt langs kuttsiden.

View fullsize

En høyere heliksvinkel (45° og oppover) øker fresens evne til å skjære istedenfor å rive og vil stort sett gi en bedre overflate, men gjør fresen skjørere og svakere. En lavere heliksvinkel (30° og lavere) gir en sterkere fres med sterkere kuttsider, men fresen lager grovere overflater siden den river mer enn den skjærer og er bedre egnet til grovbearbeiding.

View fullsize

En fres med middels heliksvinkel (mellom 30° - 45°) vil være godt egnet til allround bruk med akseptable resultater.

View fullsize

Også her lekes det med parametre for å motvirke vibrasjoner og hakking. Høy-prestasjonverktøy har ofte variable heliksvinkler på hver flute som forhindrer ytterligere resonans og bryter opp mønsteret.

View fullsize

Flere illustrasjoner hentet fra Harvey Performance. 

Krag-Jørgensen kammer-ende (links trapesgjenger!?)

View fullsize

I det siste har jeg blant annet jobbet med å lage en bit av et Krag-Jørgensen løp. Det skal simulere kammer-enden av et Krag-løp for å øve på de diverse finurlighetene som omfatter Kragen og det er god trening i prosesser man ikke gjør så ofte.

View fullsize

Krag løpet er spesielt på mange måter, som gjør det utfordrende å lage det. For det første er gjengene linksgjenget trapesgjenger. Man kan undres om hvorfor. Trapesgjenger er sterke, og det sies at dette var noe Steyr ville ha da de lagde dem. Linksgjengene kan være begrunnet med at dette var en enklere måte å maskinere gjengene på med det utstyret de hadde eller noe i den duren, men det er vanskelig å si med sikkerhet hvorfor noen av disse særegne trekkene ble brukt. Men våpenet ble oppfunnet på en tid da det var hurtig utvikling i feltet og lite var standardisert som det er i dag. Tidlige Kongsberg-produserte Krager hadde firkantgjenger.

For det andre har løpet et frest og filt spor som løfter utdrageren vekk fra patronen slik at patronen ikke skal kunne gi den et støt bakover og oppover som kan gjøre at den lange utdrageren (2 på bildet under) fyker oppover og knekker. At systemet i det hele tatt krever en slik løsning er bare et bevis på et dårlig system spør du meg, men det er nå engang sånn. 

View fullsize

Så, hvordan dreier man trapesgjenger? Dette var det første jeg måtte takle. I bunn og grunn gjøres dette ikke noe annerledes enn vanlige gjenger, men det er et par viktige momenter å ta hensyn til.

Trapesgjenger er i stor grad, mye større grad enn vanlige 60° gjenger, avhengig av et godt og riktig profilskjær. Tykkelsen på skjæret varierer med stigningen og hver stigning trenger et dedikert skjær. Man kan ikke som med 60° gjenger bruke det samme verktøyet på så og si alle stigninger. Det vil si, man kan, men det krever at man gjenger med toppsleiden i en 90° posisjon og øker bredden på kuttet med den; det er ikke "korrekt" måte å gjenge på, men det kan gjøres.

Amerikanske trapesgjenger, også kalt Acme-gjenger, har en total profilvinkel på 29° og altså en flankevinkel på 14,5°. Høyden på gjengene er halvparten av stigningen.

Men Kragens trapesgjenger er ikke 29°, de er 30°. Dette er hovedsakelig den eneste forskjellen på Acme-gjenger og metriske trapesgjenger. 

I atter et fåfengt utbrudd over blanding av standarder og enheter må jeg forbanne de som tenkte det var en god idé å oppgi metriske trapesgjenger med en stigning i tommer. Løpet skal ha 12 gjenger per tomme; 25,4/12 = 2,116, altså er stigningen litt over 2mm...

... men gjengeprofilen bruker metrisk 30° trapesform som skulle tilsi at stigningen ville vært et rundt tall. Men neida.

View fullsize

Uansett, etter å ha høylytt utåndet min oppgitthet måtte jeg finne ut hvordan formskjæret skulle være. Det er vel og bra at jeg vet stigningen, som gir meg tykkelsen på skjæret ved midten av profilen (som er halvparten av stigningen), men hvor tykk skal tuppen være? Den må jo selvsagt være tynnere for å lage selve trapesformen. 

Det finnes en enkel formel, eller rettere sagt, konstant, som kan brukes for å beregne tykkelsen ved rot og tupp av trapesgjenger:

View fullsize

"Litt" refererer her til pasning og klaring for frigang i gjengene og varierer fra kilde til kilde, men for det meste har jeg sett 0,12 mm lagt til C og 0,24 mm lagt til D.

Men denne regelen gjelder for amerikanske Acme-gjenger og vil ikke være helt overførbar til metriske gjenger. Det er bare 1° forskjell, men det kan utgjøre litt endring. Ettersom vi øker flankevinkelen vil topptykkelsen gå mot 0P ettersom det til slutt blir et punkt og ikke en flate. På motsatt side vil dette forholde gradvis gå mot 0,5 P når vi senker flankevinkelen ettersom vi nærmer oss firkantgjenger der topptykkelsen og bunnbredden er lik. Så når vi øker flankevinkelen vil topptykkelsen synke.

Jeg kom med litt tvilsom trigonometri frem til at tuppen på skjæret mitt, uten noen hensyn til rotklaring ville være 0,644mm. Dette gir meg et forhold på 0,3043. Om dette er korrekt er jeg ikke 100% sikker på, men det fungerte greit så jeg må anta at det var noenlunde innenfor.

Med denne informasjonen kunne jeg begynne å tilvirke skjæret mitt. Jeg ville prøve å planslipe skjæret mitt så det ble så nøyaktig og bra som mulig, som en øvelse i presisjon og et forsøk for å se om det er verdt bryet. Det behøves en metode å spenne opp hurtigstålet som skal slipes slik at det kan stilles vinkler i to akser samtidig. Jeg fant en gammel gud-vet-hva som kunne strammes tilstrekkelig og stilles i to vinkler. Den måtte også være magnetisk for å sitte fast på magnetbordet til plansliperen.

View fullsize

Her stilles stålet inn til 15° for å slipe den første siden.

Dessverre har vi ikke tvinge som kan stilles i vinkel, og ihvertfall ikke en som kan stilles i to, så de lesere der ute som måtte grøsse/le over løsningen på bildet over etter min proklamerte higen etter presisjon vil være berettiget, men det var den løsningen jeg fant og det funket fint.

If it's stupid and it works, it ain't stupid.

View fullsize

Trapesgjenger har også vanligvis ganske stor heliksvinkel siden stigningen er så høy i forhold til diameteren, så dette er også en vinkel som må tas hensyn til. Flankene på gjengene er såpass rette og skjæret såpass "høyt" at det er viktig å slipe inn heliksvinkelen, samt klaringsvinkler på begge sider. 

View fullsize

Disse vinklene ble stilt inn og slipt, med den ene forskjell fra normale skjær at heliksvinkelen peker mot høyre og ikke mot venstre siden gjengene er linksgjenger.

View fullsize

30° form ferdig slipt, nå gjenstod kun å slipe spissen til korrekt tykkelse og bygge inn endeklaringen.

Da det var gjort var det på tide å prøve det nye skjæret:

View fullsize

Det ser lovende ut. Utfordringen her og noe som pinte meg litt var at siden gjengene er links så er den enkleste måten å lage dem på å starte innerst og mate utover, og uten et frispor gjør dette at man blir nødt til å øke kuttdybden med en gang man starter maskinen eller presse skjæret inn i stykket før man starter maskinen. Samt at man må være veldig påpasselig og ømfintlig med startspaken når man skal finne igjen begynnelsen av kuttet inne ved roten.

Det finnes bedre måter å gjøre dette på, og dersom man ville laget linksgjenger ved å mate innover må man montere skjæret opp ned og kjøre dreiebenken "bakover".

View fullsize

Gjengene ser korrekte ut, men passer de?

View fullsize

Jada. Litt langt gjengeparti, men det var ment som en øvelse/test. Jeg endte opp med å kutte ned lengden på dette partiet og bruke det videre.

Deretter ble kammeret rømmet og resten av emnet dreid ned til spec.

View fullsize

View fullsize

Det andre litt kinkige trekket ved Krag-løpet er som nevnt rampen til utdrageren. 

View fullsize

Her benyttet jeg litt Blue Dykem (halleluja) merkefarge for opprissing og skrudde på låsekassen for å merke opp hvor sporet måtte være. Dette sporet er ikke helt sentrert.

Igjen så kan jeg ved dette stadiet bare le av min søken etter presisjon med tanke på vinkler. Å rette noe etter stablede parallellklosser er ikke optimalt, men i mangel av noen enkel måte å vinkle etter stikka (f.eks. vinkel passbiter) funket dette helt fint.

View fullsize

Grovformen til sporet ble frest ut, men siden rampen har en konveks form må det files litt til slutt.

View fullsize

Som vi kan se på bildet under skal kurven i rampen (høyre) være slik at kanten sett ovenfra blir rett (venstre).

View fullsize

Etter mye testing og justering fungerte alt som det skulle. De siste to sporene ble frest i sidene og øvelsen var ferdig og ble godkjent.

View fullsize

En meget interessant oppgave som ga meg mulighet til å prøve meg på mer viderekommen gjenging og tilpassing.

Nytt liv til en gammel arbeidshest

View fullsize

Endelig er jeg ferdig et prosjekt som er meg hjertet nært. Et prosjekt jeg har holdt på med siden skoleåret startet i fjor. Min helt egen custom Mauser 98 i .30-06 Springfield! Det ser kanskje ikke sånn ut, men den startet livet som en Karabiner 98k i den tyske hær under andre verdenskrig. En slik som er avbildet under.

View fullsize

Det er ikke min spesifikke rifle jeg holder i bildet over, det er faktisk den som ligger bak. Da jeg overtok den hadde den en gammel, sliten sporter-stokk på seg, men den startet som sagt livet på samme vis som den jeg holder her. Mange av disse riflene som ble liggende igjen etter krigen ble tatt i bruk i Hæren, men kort etter konvertert til .30-06 og gitt til Heimevernet da vi adopterte M1 Garand. På ett eller annet tidspunkt hadde den blitt kamret om til .308 Winchester (som noen få ble da dette ble NATO standard) som jeg ikke fant ut før jeg allerede var på skytebanen og hadde kjøpt .30-06 skudd. Ugh...

Men jeg trengte et våpen til både trening og jakt og tenkte det var en fin anledning til å ha et eget våpen jeg kunne bruke på skytedagene vi skulle ha. Prosjektet startet enkelt nok med den simple endring at jeg ville ha den i .30-06 og en ny stokk. Det ene førte til det andre og plutselig er det eneste originale igjen på børsa låsekassa og sluttstykket. Som er blitt tungt modifisert de og.

Det har vært en lang og lærerik reise med oppturer og nedturer.

Kamring og dreiing av nytt løp

Aller først fjernet jeg selvsagt løpet. Det satt godt fast så låsekassa måtte varmes opp for å løsne det.

View fullsize

Den originale løpsprofilen er fler-steget, eller trappet, og personlig er jeg ikke noen tilhenger av designet. For ikke å nevne at det ikke lar seg gjøre å kammre om et .308 løp til .30-06 uten å fjerne en del av kammer-enden siden tykkelsen på .30-06 hylsen er mindre der den treffer .308 skulderen enn .308 er, slik at det ville dannet seg en grop i kammeret her som ville gjort at hylsen ville blitt deformert/sprukket/satt seg fast ved avfyring.

View fullsize

Det er ingen spesiell grunn til at jeg ville ha .30-06 annet enn at jeg liker kaliberet og det en kraftig og allsidig patron. Riflen skal brukes til storviltjakt og langholdsskyting så et relativt grovt kaliber føltes riktig. Det går jo mye på følelser dette; og ikke nødvendigvis på tross av fakta.

Jeg fikk tak i en hylse som er et "adapter" som tilpasses diverse låsekasser og omgjør den til en delvis standardisert festemetode slik at våpenet blir et 'systemvåpen', altså at brukeren kan enkelt skifte løp dersom et annet kaliber kreves eller ønskes brukt i samme våpen.

View fullsize

Kammeret er selvsagt fortsatt i løpet, men det stikker på en måte ut av løpet og tres inn i hylsen. På bildet over er hylsen satt på feil vei for å sjekke pasning. Denne krevde litt å lage; selve pasningen vist over hadde kun 0,03 millimeter unilateral negativ toleranse.

View fullsize

Over kan vi se hylsen skrudd på løpet og gjenger slått i hylsen for å passe i låsekassen (under).

View fullsize

Deretter brotsjes (les: rømmes) kammeret med hele smæla skrudd sammen.

View fullsize

Etter inspeksjon og testskyting av det nye kammeret viste det seg at jeg hadde fått en rivning i metallet under prosessen som hadde etterlatt seg et dypt sår inne i kammeret og som deformerte patronen som vist på bildet under. Dette gjorde den svært vanskelig å få ut, men det gikk heldigvis med bare litt makt. Den dårlige nyheten var jo selvsagt at jeg måtte gjøre alt på nytt, inkludert å lage det presise hylse-partiet om igjen også... 

View fullsize

Men andre gangen gikk det knirkefritt og resultatet ble tilfredsstillende.

Under dreier jeg ned det nye, nå ferdig kammrede, løpsemnet fra Lothar Walter. I første omgang kun ren masseavvirkning for å tynne løpet.

View fullsize

Konusdreiing for å fullføre løpsprofilen. Her brukte jeg brille for å minimere vibrasjoner og optimalisere maskinert overflatefinhet før puss.

View fullsize

Løpet behøver ikke være så veldig tykt, men et tykkere løp bidrar til økt presisjon. Jeg lot løpet være ganske tykt fordi jeg vill ha høy presisjon og løpet skulle uansett flutes for å fjerne noe vekt. Den koniske profilen på løpet bidrar til et slankere og helhetlig visuelt inntrykk med tanke på perspektiv.

Fluting

Jeg flutet løpet, hovedsakelig for utseende, men også for å redusere vekt. Dette var stort sett en langsom og kjedelig prosess siden matehastigheten var så lav. Når ett kutt tar ca 15 min og 5 fluter på 3-4 kutt per flute... det tok tid. Men verktøyet var flunkende nytt og prosessen ny for meg så jeg tok det heller litt med ro enn å forhaste meg. Finishen på flutene ble også veldig bra.

View fullsize

På tross av den langsomme prosessen var det en svært interessant og lærerik prosess. I bildet over klokker jeg inn løpet slik at kuttsiden er parallell med X-aksen. Siden løpet er konisk må det spennes opp litt på skrå for at flutens tykkesle skal bli jevn. Det ble spent opp i et delehode og en senterspiss med en vinkelplate som støtte bak. En liten innretning med et spor i satt rundt løpet og ble brukt for å trekke mot vinkelplaten og holde det stramt på plass. 

View fullsize

Det viktigste her er at flutene blir symmetrisk, så den første fluten må stilles inn i forhold til hvordan løpet sitter i låsekassa. Jeg monterte det fast i rifla og merket opp med en av de andre fresene hvor midten/toppen av løpet var. Deretter monterte jeg det opp i oppspenningen over og brukte en høyderissemåler/rissefot får å vise midten av løpet og roterte delehodet til den rissede linjen og høyderissemåleren møttes. Jeg gjorde også noen små testkutt for å verifisere at verktøyet fulgte denne linjen. Nå skulle den første fluten teoretisk sett bli midt oppå løpet.

View fullsize

Jeg lagde som nevnt 5 fluter, av den enkle grunn at det gjorde at jeg slapp å flytte vinkelplaten for hver rotasjon, siden med et oddetall fluter vil løpet alltid hvile mot vinkelplaten på en ribbe og ikke på en flute. Jeg er av den tro at et partall fluter, som er fullstendig symmetrisk, vil gi et stivere løp siden den totale tykkelsen mellom ribbene blir større enn med et oddetall fluter, men det skal tydeligvis ikke utgjøre så stor forskjell.

Et annet viktig moment å tenke på er hvordan løpet er tilvirket. Hvordan det er laget, om det er varmhamret eller kaldhamret eller om riflingene er påført i etterkant med en "button" som dras gjennom pipa kan påvirke hvordan løpet reagerer på å bli flutet. Det kan hende det innfører spenninger ved å lage en hel dyp flute på en gang før man tar den neste, eller det kan gå fint, men man kan trenge å ta alle kutt av samme dybde før man øker kuttdybden for å opprettholde rettheten i pipa, men det var heldigvis ikke et problem for meg med dette løpet.

Låsekassen

Mye ble gjort med selve låsekassen og sluttstykket.

Mest interessant av alt er vel en idé jeg fikk av mine mentorer på XXL. Mauser-låsekassen er relativt fleksibel og svak p.g.a utsparingen til tommelen som er der for at våpenet skal kunne bli ladet med stripper-clips. Så tanken er å sveise igjen dette hullet for å stive opp kassa. Hvilket jeg gjorde. 

View fullsize

Jeg lagde en bit av vanlig maskinstål som passet sånn høvelig greit i hullet med litt overmål og MIGet den fast utenpå og inni. Deretter freste jeg vekk det verste og avsluttet med fil. 

View fullsize

View fullsize

Utenom det ble det tilvirket en ny picatinny-skinne som jeg har skrevet om tidligere og nye monstasjehull boret og gjenget.

Nytt avtrekk ble installert, Timney FWD med avtrekkersikring. Siden jeg nå hadde sikring på avtrekkeren ble den originale direkte sikringen på shroud'en fjernet og ny shroud ble kjøpt. Dette er riktignok litt mindre sikkert, men fortsatt sikkert nok.

View fullsize

Utdrageren og bolt-stoppen ble blå-anløpt og jeg monterte en ny selvdesignet hevarm.

Jeg kjøpte også Superior Shooting speedlock-system som er et tennstempel av titan eller stål og aluminium med en ny fjær i krom-silikon legering. Dette kan senke tiden fra avtrekk til skuddet går med flere millisekunder.

View fullsize

 

Rekylbrems

Jeg lagde min egen rekylbrems som er uthulet og plugget igjen for å fange og redirigere så mye av munninggassene som mulig.

View fullsize

Den fanger gassene og omdirigerer dem ut til sidene, oppover og bakover. Også ser den tøff ut.

View fullsize

View fullsize

 

Cerakote

Da alt var ferdig var det på tide å cerakote løp og låskasse, samt andre smådeler. Når det kom til løpet ville jeg ha blanke fluter, så disse ble maskert og endene av løpet plugget.

View fullsize

Cerakote og Durakote er en form for lakk som inneholder keramiske partikler og herder over flere dager og produserer et motstandsdyktig og slitesterkt lag. Det er viktig ved påføring at det som skal sprayes er glass-/sandblåst, avfettet og tørt. Det påføres i èn omgang med mange lette lag, mye som annen pulverlakkering.

View fullsize

Nydelig.

View fullsize

Stokk og bedding

I utgangspunktet hadde jeg tenkt til å lage min egen stokk i tre, men siden jeg satte på skinne på låsekassa ville det bli knotete å fylle på ammunisjon i magasinet, så jeg ville ha en løsning med uttakbare boksmagasin. Det var noen greie løsninger der ute og planen var å benytte AICS magasiner med en long-action underbeslag, men det viste seg å være en veldig vanskelig kombinasjon å finne for Mauser. Så jeg endte opp med en AA98, en glassfiber-forsterket polymer-stokk fra Archangel. Denne har mange justeringsmuligheter, er spesialtilpasset M98 og kommer med magasinløsning og et magasin. Jeg kjøpte også to ekstra magasiner, fordi hva er poenget med boksmagasinsystem med bare ett magasin?

Men selv om den kommer ferdig tilpasset var det ikke bra nok for meg. Ikke bare måtte jeg utvide løpskanalen til å passe det nye løpet mitt, jeg ville også bedde stokken. Det vil si å fylle i et epoxyharpiks i stokken for så å presse og skru fast låsekassa med dette stoffet i mellom og la det herde. Dette vil lage et eksakt avtrykk av låsekassa i stokken og den vil ligge godt og solid og vil ikke kunne røre på seg. Det vil også hindre at man drar inn spenninger i låsekassa når man skrur den i stokken som igjen vil bidra til økt presisjon.

View fullsize

Første steg er å rufse opp innsiden der epoxyen skal sitte. Det er kun nødvendig å bedde rundt festepunktene, dvs. rundt skruene, men det må der beddes helt opp til kanten av stokken og spesielt i rekylopptaket, vanligvis den utstikkende flaten ved den fremste skruen.

Det er viktig å lage dype og ru spor her slik at beddingen fester seg godt til stokken. Mange små ikke-parallelle kriker og kroker som limet kan flyte inn i lager et godt feste.

View fullsize

Deretter smøres låsekassen, skruene og alt annet som ikke skal ha lim på seg inn med f.eks. skokrem slik at limet ikke fester seg til annet enn stokken. Så blandes beddemassen som er en blanding av lim og herder, i dette tilfellet i et forhold på 1:4 herder/lim. Vi blandet her 20g lim og 5g herder. Krydre med litt svart fargepulver etter smak. Finhakk en håndfull isolasjon og ha i. Rør godt.

View fullsize

Man ønsker en konsistens slik at det ikke flyter og drypper av rørepinnen. Glassfiberet gir limet styrke og struktur.

Massen legges på og presses godt ned og inn i alle de tidligere nevnte kriker og kroker. En liten rygg av masse legges midt på for å hindre at det fanges luftbobler og som automatisk presses ut fra midten og sørger for en jevn spredning.

View fullsize

Man skrur så fast låsekassen, men ikke så hardt at de spenningene vi prøver å unngå blir bygget inn i beddingen. Så vi strammer til det stopper og så løsner opp til låsekassen ikke stiger mer.

View fullsize

Etter at det er herdet kan de største ansamlingene pirkes av og så kan mekanismen røskes ut av stokken.

View fullsize

Skruehullene kan trenge å bores opp siden det har samlet seg beddemasse i skruekanalene som kan gjøre de vanskelig å få inn skruene ordentlig.

View fullsize

 

Voila!

View fullsize

View fullsize

View fullsize

View fullsize

View fullsize

Annet tilbehør som er brukt:

• Accu-Tac LR-10 tofot
• Accu-Shot Mid-Range monopod
• Vortex Viper PST 6-24x50 EBR-1 MRAD kikkertsikte
• Daniel Defense QD sling mount
• Magpul MS4 Dual QD GEN2 reim

View fullsize

Nå er jeg fornøyd og veldig glad! Jeg gleder meg til å ta den med på skytebanen og virkelig sette både den og meg på prøve.