Krag-Jørgensen kammer-ende (links trapesgjenger!?)
/I det siste har jeg blant annet jobbet med å lage en bit av et Krag-Jørgensen løp. Det skal simulere kammer-enden av et Krag-løp for å øve på de diverse finurlighetene som omfatter Kragen og det er god trening i prosesser man ikke gjør så ofte.
Krag løpet er spesielt på mange måter, som gjør det utfordrende å lage det. For det første er gjengene linksgjenget trapesgjenger. Man kan undres om hvorfor. Trapesgjenger er sterke, og det sies at dette var noe Steyr ville ha da de lagde dem. Linksgjengene kan være begrunnet med at dette var en enklere måte å maskinere gjengene på med det utstyret de hadde eller noe i den duren, men det er vanskelig å si med sikkerhet hvorfor noen av disse særegne trekkene ble brukt. Men våpenet ble oppfunnet på en tid da det var hurtig utvikling i feltet og lite var standardisert som det er i dag. Tidlige Kongsberg-produserte Krager hadde firkantgjenger.
For det andre har løpet et frest og filt spor som løfter utdrageren vekk fra patronen slik at patronen ikke skal kunne gi den et støt bakover og oppover som kan gjøre at den lange utdrageren (2 på bildet under) fyker oppover og knekker. At systemet i det hele tatt krever en slik løsning er bare et bevis på et dårlig system spør du meg, men det er nå engang sånn.
Så, hvordan dreier man trapesgjenger? Dette var det første jeg måtte takle. I bunn og grunn gjøres dette ikke noe annerledes enn vanlige gjenger, men det er et par viktige momenter å ta hensyn til.
Trapesgjenger er i stor grad, mye større grad enn vanlige 60° gjenger, avhengig av et godt og riktig profilskjær. Tykkelsen på skjæret varierer med stigningen og hver stigning trenger et dedikert skjær. Man kan ikke som med 60° gjenger bruke det samme verktøyet på så og si alle stigninger. Det vil si, man kan, men det krever at man gjenger med toppsleiden i en 90° posisjon og øker bredden på kuttet med den; det er ikke "korrekt" måte å gjenge på, men det kan gjøres.
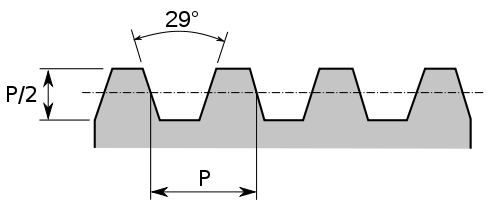
Amerikanske trapesgjenger, også kalt Acme-gjenger, har en total profilvinkel på 29° og altså en flankevinkel på 14,5°. Høyden på gjengene er halvparten av stigningen.
Men Kragens trapesgjenger er ikke 29°, de er 30°. Dette er hovedsakelig den eneste forskjellen på Acme-gjenger og metriske trapesgjenger.
I atter et fåfengt utbrudd over blanding av standarder og enheter må jeg forbanne de som tenkte det var en god idé å oppgi metriske trapesgjenger med en stigning i tommer. Løpet skal ha 12 gjenger per tomme; 25,4/12 = 2,116, altså er stigningen litt over 2mm...
... men gjengeprofilen bruker metrisk 30° trapesform som skulle tilsi at stigningen ville vært et rundt tall. Men neida.
Uansett, etter å ha høylytt utåndet min oppgitthet måtte jeg finne ut hvordan formskjæret skulle være. Det er vel og bra at jeg vet stigningen, som gir meg tykkelsen på skjæret ved midten av profilen (som er halvparten av stigningen), men hvor tykk skal tuppen være? Den må jo selvsagt være tynnere for å lage selve trapesformen.
Det finnes en enkel formel, eller rettere sagt, konstant, som kan brukes for å beregne tykkelsen ved rot og tupp av trapesgjenger:
"Litt" refererer her til pasning og klaring for frigang i gjengene og varierer fra kilde til kilde, men for det meste har jeg sett 0,12 mm lagt til C og 0,24 mm lagt til D.
Men denne regelen gjelder for amerikanske Acme-gjenger og vil ikke være helt overførbar til metriske gjenger. Det er bare 1° forskjell, men det kan utgjøre litt endring. Ettersom vi øker flankevinkelen vil topptykkelsen gå mot 0P ettersom det til slutt blir et punkt og ikke en flate. På motsatt side vil dette forholde gradvis gå mot 0,5 P når vi senker flankevinkelen ettersom vi nærmer oss firkantgjenger der topptykkelsen og bunnbredden er lik. Så når vi øker flankevinkelen vil topptykkelsen synke.
Jeg kom med litt tvilsom trigonometri frem til at tuppen på skjæret mitt, uten noen hensyn til rotklaring ville være 0,644mm. Dette gir meg et forhold på 0,3043. Om dette er korrekt er jeg ikke 100% sikker på, men det fungerte greit så jeg må anta at det var noenlunde innenfor.
Med denne informasjonen kunne jeg begynne å tilvirke skjæret mitt. Jeg ville prøve å planslipe skjæret mitt så det ble så nøyaktig og bra som mulig, som en øvelse i presisjon og et forsøk for å se om det er verdt bryet. Det behøves en metode å spenne opp hurtigstålet som skal slipes slik at det kan stilles vinkler i to akser samtidig. Jeg fant en gammel gud-vet-hva som kunne strammes tilstrekkelig og stilles i to vinkler. Den måtte også være magnetisk for å sitte fast på magnetbordet til plansliperen.
Her stilles stålet inn til 15° for å slipe den første siden.
Dessverre har vi ikke tvinge som kan stilles i vinkel, og ihvertfall ikke en som kan stilles i to, så de lesere der ute som måtte grøsse/le over løsningen på bildet over etter min proklamerte higen etter presisjon vil være berettiget, men det var den løsningen jeg fant og det funket fint.
If it's stupid and it works, it ain't stupid.
Trapesgjenger har også vanligvis ganske stor heliksvinkel siden stigningen er så høy i forhold til diameteren, så dette er også en vinkel som må tas hensyn til. Flankene på gjengene er såpass rette og skjæret såpass "høyt" at det er viktig å slipe inn heliksvinkelen, samt klaringsvinkler på begge sider.
Disse vinklene ble stilt inn og slipt, med den ene forskjell fra normale skjær at heliksvinkelen peker mot høyre og ikke mot venstre siden gjengene er linksgjenger.
30° form ferdig slipt, nå gjenstod kun å slipe spissen til korrekt tykkelse og bygge inn endeklaringen.
Da det var gjort var det på tide å prøve det nye skjæret:
Det ser lovende ut. Utfordringen her og noe som pinte meg litt var at siden gjengene er links så er den enkleste måten å lage dem på å starte innerst og mate utover, og uten et frispor gjør dette at man blir nødt til å øke kuttdybden med en gang man starter maskinen eller presse skjæret inn i stykket før man starter maskinen. Samt at man må være veldig påpasselig og ømfintlig med startspaken når man skal finne igjen begynnelsen av kuttet inne ved roten.
Det finnes bedre måter å gjøre dette på, og dersom man ville laget linksgjenger ved å mate innover må man montere skjæret opp ned og kjøre dreiebenken "bakover".
Gjengene ser korrekte ut, men passer de?
Jada. Litt langt gjengeparti, men det var ment som en øvelse/test. Jeg endte opp med å kutte ned lengden på dette partiet og bruke det videre.
Deretter ble kammeret rømmet og resten av emnet dreid ned til spec.
Det andre litt kinkige trekket ved Krag-løpet er som nevnt rampen til utdrageren.
Her benyttet jeg litt Blue Dykem (halleluja) merkefarge for opprissing og skrudde på låsekassen for å merke opp hvor sporet måtte være. Dette sporet er ikke helt sentrert.
Igjen så kan jeg ved dette stadiet bare le av min søken etter presisjon med tanke på vinkler. Å rette noe etter stablede parallellklosser er ikke optimalt, men i mangel av noen enkel måte å vinkle etter stikka (f.eks. vinkel passbiter) funket dette helt fint.
Grovformen til sporet ble frest ut, men siden rampen har en konveks form må det files litt til slutt.
Som vi kan se på bildet under skal kurven i rampen (høyre) være slik at kanten sett ovenfra blir rett (venstre).
Etter mye testing og justering fungerte alt som det skulle. De siste to sporene ble frest i sidene og øvelsen var ferdig og ble godkjent.
En meget interessant oppgave som ga meg mulighet til å prøve meg på mer viderekommen gjenging og tilpassing.