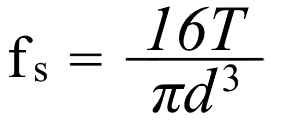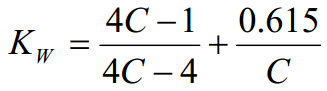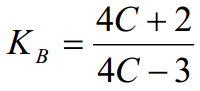Dreieverktøy og skjær

/

To av oppgavene vi har hatt er å slipe hurtigstål-skjær til dreiebenken. Vi skulle slipe et gjengeskjær og et kronestål. Begge er formverktøy som påfører en profil i arbeidsstykket:

Gjengeskjæret over ble slipt for hånd uten noen form for støtter og sjekket med et slipelære.

Skjæret er 60° slik at hver kuttside er 30° fra senterlinjen.

Klaringsvinklene er like på begge sider og skjæret har ingen innebygd vinkel siden heliksvinkelen for 60° gjenger er så liten at den kan ignoreres.

Dette verktøyet profilerer i X-retningen.

02.jpg

Kronestålet er et formverktøy på den mer tradisjonelle måten i det at den påfører en unormal form på arbeidstykket. Dette verktøyet har flere bruksmåter, men hovedbruken er å krone munningen på løp som jeg har snakket om tidligere. Verktøyet settes slik at spissen er inne i løpet og toppen av buen ligger midt på godset mellom innsiden og utsiden. Verktøyet føres så inn langs Z-aksen og påfører profilen på munningen. Dette vil da resultere i en klassisk jakt-kroning. Verktøyet kan også beveges litt frem å tilbake på X-aksen for å endre kroneprofilen. Dersom en 11° kroning ønskes kan tuppen av skjæret brukes til dette.

Weatherby-Vanguard-308Win-0006-crown.jpg

Jeg tenkte jeg skulle benytte anledningen til å skrive litt om typer skjær og bruksområder, fremstilling og gjenkjenning.

Det finnes hovedsaklig to typer dreieverktøy; hurtigstål og hardmetall.

Hurtigstål-blanks

Hardmetall-inserts

Hurtigstål

Hurtigstål er et høy-legert stål med et høyt karboninnhold som gjør det svært hardt, men sprøtt. Det tåler høyere temperaturer enn vanlig høy-karbon stål uten å miste hardheten sin, vanligvis opp til 500-600 °C. Denne motstandsdyktigheten til temperatur heter "red hardness" på engelsk. Det kalles hurtigstål fordi det er i stand til å bearbeide metall raskere og ved høyere turtall enn annet renere stål. Det er tilført stoffer som lager legeringer som forbedrer egenskapene og levetiden til verktøyet. De vanligste tilføringene er wolfram (W), molybden (Mo), krom (Cr), vanadium (V), kobolt (Co), mangan (Mn) og silikon (Si).

De to vanligste typene hurtigstål kategoriseres i to grupper: T-type og M-type, for hovedsakelig Tungsten(wolfram)-tilføringer og Molybden-tilføringer respektivt. T1 er et hovedsakelig wolfram-legert stål mens M2 er et hovedsakelig molybden-legert stål. Tallet bak bokstaven relaterer ikke nødvendigvis til noe spesielt med den ståltypen, det er først og fremst for å skille dem fra hverandre.

Det finnes uendelig mange varianter og typer hurtigstål, men de vanligste er oppført i tabellen under:

high_speed_chart.jpg

Som vi kan se på tabellen har M serien mye molybden og T serien mye wolfram, men wolfram er den klassiske og tidligere vanligste tilføringen, så M serien har mer wolfram enn T serien har molybden. Kobolt kan også tilføres for å øke levetiden og temperaturmotstanden, dette er da ofte opplyst på stålet. Vanlige benevnelser for dette er HSSE, HSS-E eller HSS-Co.

Wolfram er et tungt og sterkt, sjeldent metall, og har det høyeste smeltepunktet av alle elementer som er oppdaget, ved 3422 °C. Bedre kjent som Tungsten i engelsktalende land etter svensk tung sten, hvem skulle trodd... Wolfram brukes til mye rart, men mesteparten av verdens wolfram-utvinning går til produksjon av wolfram-karbid som brukes i hardmetall.

Molybden er et annet sterkt metall med et veldig høyt smeltepunkt ved 2623 °C. Det binder seg lett og lager harde og sterke bindinger i legeringer. Molybden opplever veldig liten termisk ekspansjon ved høye temperaturer.

Hurtigstål har stort sett en hardhet på over 60 HRC opp til ~67 HRC.

 

Sliping av hurtigstål

Hurtigstål brukes i veldig mange sponfraskillende verktøy, som bor, gjengetapper, freser, rømmere, brotsjer, etc. Men hurtigstål beregnet for bruk i dreiebenker leveres som blanke, uformede biter i mange ulike størrelser og former.

Fordelen med å bruke slike hurtigstål-blanks er at det kan slipes og formes til det formålet man behøver og kan skjærpes når det blir sløvt. 

Et typisk hurtigstål-skjær kan se slik ut:

Disse kalles hovedsakelig "single point cutters" på engelsk, ettersom det bare er ett punkt eller side som kutter, i motsetning til f.eks. et bor der det er to sider som kutter samtidig.

Det finnes mange ulike former etter hvilken operasjon som skal utføres:

Hvilket verktøy som er beregnet for hvilken retning og hva det eventuelt heter kan være litt forvirrende, men som en regel kan vi si at dersom man står mot dreiebenken er høyre-verktøy ikke verktøy som peker mot høyre eller har kuttsiden på høyre, men verktøy som er beregnet på å bevege seg fra høyre mot venstre, altså har de den kuttende siden på venstre.

 

Når det kommer til å faktisk slipe dem er det en del ting som er viktig å forstå:

Skjæret må selvsagt ha klaring fra alle sider bortsett fra kuttsiden slik at skjæret faktisk kan føres inn i materialet uten at noe annet enn kuttsiden treffer arbeidsstykket. Disse formene kan være komplisert å slipe siden man må til tider holde styr på 3 vinkler samtidig.

Det er egentlig ingen fasit på hvilken rekkefølge disse flatene bør slipes i, men som hovedregel kan vi si at:

  • Endeklaringen slipes først. Dette er første del av spissvinkelen: endeklaringen og endeklaringsvinkelen, som slipes samtidig:

Disse to vinklene holdes samtidig. Stålet føres rundt i sirkel mens det holdes stødig til hele den slipte flaten er uniform. Stålet kan også presses inn i steinen og holdes der, men vær obs på at endeklaringen da vil få en slak kurve som er lik radien til slipesteinen og vil ikke bli like sterk.

PROTIP: Det er en fordel at slipemerkene går langs med dreieretningen og ikke lager "fartsdumper" for sponet eller arbeidstykket.

Resultat:

  • Deretter slipes andre del av spissvinkelen og første del av eggvinkelen; klaringsvinkelen og innstillingsvinkelen.

Jeg pleier å holde hele stålet litt på skrå sett forfra mot slipesteinen, vanligvis i samme vinkel som endeklaringen. Ikke egentlig nødvendig, men det gjør slipingen på klaringsvinkelen parallell med endeklaringen, som jeg liker.

PROTIP: Spissere tupp (spissvinkel) vil tåle mindre og gi grovere overflate, spesielt uten neseradius, men kan være nødvendig for å bl.a. lage skarpe innvendige hjørner.

Resultat:

  • Så slipes andre del av eggvinkelen; sponvinkelen og hellingsvinkelen. Denne slipes ofte også på skrå på samme måte som over slik at slipingen blir parallell med endeklaringsvinkelen.

PROTIP: Skarpere sponvinkel og hellingsvinkel vil stort sett føre til en mer 'skjærende' operasjon i stedet for en 'rivende' bevegelse, som vil gi finere overflate. (Kjølevæske vil også drastisk øke overflatefinheten fordi det bl. a. skyller vekk mikro-spon som riper opp overflaten.)

Resultat:

  • Etter dette gjenstår kun å slipe eller hone inn neseradien:

Et grunnleggende og enkelt dreieskjær.

PROTIP: En enkel sponbryter er også å anbefale: En liten grop på tvers av sponvinkelen eller hellingsvinkelen vil øke den effektive eggvinkelen og bidra til at sponet krøller seg og bryter av uten å bli for langt, men denne kan også begrense bruken til skjæret. Sponbryteren burde bli trangere jo lenger vekk fra skjærpunktet den går.

Det kan også lønne seg (for den siste prikken over i'en) å hone eggen med en slipesten eller lignende for en knivskarp egg. Hvis DU skjærer deg på den kan du vedde på at den vil skjære stålet som smør. 

 

 

Hardmetall

Hardmetall er egentlig ikke et metall, det er keramisk bundet wolfram-karbid. Karbider er stoffer der karbon binder seg med andre elementer i veldig strukturerte og solide former. Hardmetall blir ofte omtalt kun som "karbid", men det er teknisk sett en forenkling av "cemented tungsten carbide" ettersom "karbid" som sagt er et fellesbegrep for flere andre materialer som f.eks. titankarbid og tantalkarbid som også brukes til å lage dreieskjær.

Wolfram-karbid (WC) er et veldig hardt materiale, nesten like hardt som diamant, men det er vanskelig å forme. Hardmetall-verktøy er derfor wolfram-karbid blandet med et bindemiddel som sammen sintres, som er en prosess der materialet presses sammen og varmes ved høy temperatur, men uten at det blir flytende. Det lages derfor mange små granuler som pakkes tett sammen og binder seg sammen med hverandre ved hjelp av et middel, vanligvis kobolt.

Denne prosessen smelter det delvis og gjør at det binder seg godt i veldig sterke formasjoner. Derav "cemented".

De tre hovedstadiene ved sintering.

Andre materialer som brukes i produksjon av dreieskjær er bl.a. syntetisk diamant og bornitrid, men sementerte karbider er vanligst.

 

Når vi snakker om hardmetall tenker nok de fleste på utbyttbare karbidskjær (indexable carbide inserts) (høyre), men de finnes også som fastmonterbare hele karbid-biter som varm-loddes fast til en bit med hurtigstål (under.)

Z1x5uupcpEx--n.jpg

Disse verktøyholderne (brazed carbide tooling) kan være tricky å lage så de fåes kjøpt i ISO standarder:

Noen av disse fåes også i venstre og høyre konfigurasjon. Karbid-bitene brukt her har ganske enkel geometri og er relativt billige, men mer komplisert å skifte ut og er derfor ikke så veldig vanlig, spesielt ikke hos store industrielle fabrikanter.

Mer utbredt, blant både industri og hobbyister, er vendeskjær:

Disse har mange fordeler som at de:

  • Arbeider ved høyere skjærehastigheter som gjør at de kan kjøre på økt matehastighet og gjør dem godt egnet til "high speed machining" (HSM) / "high velocity machining" (HVM).
  • Har relativt lang levetid, kombinert med at de kan løsnes raskt og vendes eller vris til en ny kuttside på samme skjær.
  • Kan raskt byttes ut når hele skjæret er brukt opp som bidrar til mindre 'downtime' for maskinen eller firmaet.
  • Gir stort sett finere overflate rett fra maskinen enn HSS.

Men det er også ulemper:

  • De er ikke like egnet til å gjøre avbrutte kutt, som hvis man dreier over borrede hull eller lignende, karbid liker et konstant og jevnt trykk, men de tåler til gjengjeld veldig mye av det.
  • De er ikke like skarpe som HSS kan bli, som kan gjøre det utfordrende å ta kutt med svært liten kuttdybde med god overflatefinhet. Hardmetall foretrekker ofte å ta litt mer materiale av gangen.

En viktig ting med hardmetall er at man trenger en spesifikk holder til et spesifikt skjær, man kan ikke, i motsetning til HSS, bruke en hvilken som helst holder til alle skjær. Bruker man WNMG skjær må man bruke WNMG holder (f.eks. en MWLNR).

Typer skjær og hvordan de defineres er selvfølgelig en ISO standard ♥ ISO 1832:

Den første bokstaven definerer fasongen på skjæret.

Det er feil å si at en av disse definerende bokstavene er viktigst siden alle er like viktige, men... dette er den viktigste. Du får ikke bestilt noe med bare denne, men det er en start.

Disse er relativt logisk organisert der bokstaver ofte er basert på den første bokstaven i formen, sånn som H, O, P, S, T, R.

Når det kommer til alle de forskjellige variantene av grader på rombe og parallellogram er man bare nødt til å slå det opp.

I eksempelet over er formen W et såkalt 'trigon' som i bunn og grunn er tre 80° trekanter satt sammen til en likesidet trekant-form.

Den andre bokstaven representerer endeklaringen på skjæret.

Akkurat som med hurtigstål så blir skjæret svakere jo mer endeklaring det har, men det kommer ofte til på flere steder og kan jobbe på ting med større diameter (eller kutte høyere over senter).

Den største klaringen er G på 30° og den minste er N som er helt rett / flat med 0°. Disse N-skjærene har ofte endeklaringen bygget inn i holderen:

 

Bokstav nummer tre definerer toleransene til skjæret. Finere toleranser koster selvsagt mer.

Vi er enda ikke kommet til størrelsen på skjæret, det er dekket av posisjon 5 og 6, men det er viktig å oppgi toleranseklassen til skjæret. Dette er da standardisert i følge tabellen over.

Toleransene er mye av det samme, men varierer på hvilket punkt av skjæret som er mest nøyaktig (tykkelse, total størrelse, lengde til egg).

Med toleranse M ser vi at toleransene er relativt store, der total størrelse og lengde til egg er viktigst for denne toleranseklassen. Disse toleransene kan være spesielt viktig i CNC-maskiner der skjæret byttes ut og foventes å produsere like deler som det gamle skjæret uten rekaliberering.

I ANSI standarden er dette mye det samme, men oppgitt i tusendels tommer.

 

Den fjerde bokstaven representerer flere ting; festemåte og sponbryter.

Herunder er alle variasjoner av følgende muligheter: sylindrisk hull, forsenket hull (1 eller 2 sider, samt flere typer forsenkning), sponbryter (1 eller 2 sider), ikke hull, ikke sponbryter.

Skjær med endeklaring noe annet enn 0° kan vanligvis ikke vendes og har derfor ikke noen sponbryter eller forsenkning på andre siden. Skjær uten forsenket hull (kun sylindrisk) er ofte festet til holderen med en låsepinne og/eller klemme.

Nå over til det som virkelig kan frustrere og forvirre: De første to tallene i posisjon 5 bestemmer størrelsen til skjæret ved Inscribed Circle (IC) som er den største sirkelen som får plass i skjæret rundt senter uten at noen del av sirkelen stikker utenfor OG/ELLER lengden av kuttesiden (L).

Alt dette er som sagt egentlig en ANSI standard som er blitt slurpet opp av ISO, og det har jeg ikke noe problem med, det er en grei standard, men da ISO tok den i bruk var produkter allerede etablert i... ikke tusendels tommer, NEIDA, antall 1/16 tommer som går i sirkelen... og ISO valgte derfor å definere noen nye størrelser i millimeter, men også beholde disse tallene i tabellene som standard. Så selv om disse tallene egentlig burde være en metrisk verdi i millimeter, så er de ikke alltid det og det er derfor spesielt viktig at denne verdien slås opp.

Så i eksempelet over, der den innskrevne sirkelen i skjæret skal være en 06 så vil det si 6/16", som er 9,525 mm.

Kan vi aldri få ha en logisk og uniform standard? Man mister litt motet...

Det er en morsom historie angående hvordan Amerika nesten gikk over til metrisk da det enda var en ung nasjon. I 1793 fant regjeringen av de nylig forente stater ut at de trengte et nytt standardisert målestystem ettersom statene fremdeles var relativt fragmentert og brukte forskjellige systemer som gjorde mellomstatlig handel og samarbeid vanskelig. Så på oppfordring av Thomas Jefferson, som også likte 10-tallssystemet, ble en fransk vitenskapsmann ved navn Joseph Dombey sendt over Atlanteren med en kobberstang som var ca. 3 fot lang og en kobbervekt som veide ca. 2 pund. Dette var selvsagt fysiske representasjoner og standarder av det, på den tiden under utvikling, metriske system som var 1 meter og 1 kilo respektivt. Han skulle hjelpe Jefferson å overtale kongressen til å adoptere det metriske system. Men på vei over havet møtte de på en storm som sendte skipet deres lengre sør, nærmere Karibien. Der ble han og skipet tatt til fange av britiske pirater som prøvde å kreve løsepenger for Dombey, men dessverre døde han i fangenskap. Tingene han hadde med seg var ikke av interesse for piratene så de ble auksjonert bort og etterhvert fant kiloet veien til en amerikansk landmåler ved navn Andrew Ellicott. Det gikk i arv til 1952 da etterkommere av Ellicott donerte det til det som kom til å bli NIST (National Institute of Standards and Technology). 

Det er riktignok ikke det eneste forsøket på å importere rasjonalitet til Amerika, men det kunne gjort en forskjell. We will never know.

 

Tallene i posisjon 6 representerer tykkelsen på skjæret. Mye av det samme gjelder her som i posisjon 5, men vi har mer frustrasjon i vente.

I eksempelet over er skjæret definert som 04 som MAN SKULLE TRO vil tilsi 4/16" men det blir 6,35mm som ikke stemmer med denne fabrikantens tabeller, så hva er det som skjer? Det var noens glupe idè at når det kommer til tykkelse så skal det brukes tomme-verdier, men tallet skal representere den nærmeste 1/16 tomme-verdien der det første tallet i millimeter-konverteringen blir 4.

3/16" blir 4,76mm så der har vi svaret. Kjempelogisk.

Avvik fra denne regelen desgineres med en bokstav i stedet for 0, vanligvis T.

Det er viktig å notere seg at tykkelsen måles fra bunnen av skjæret og opp til skjærepunktet/eggen.

Den siste pålagte informasjonen, posisjon 7, representerer neseradien til skjæret. Her er det heldigvis litt mer logikk inne i bildet og de to tallene i denne posisjonen er direkte overførbare til en radius i millimeter. 

I eksempelet over er tallene 08 som betyr at neseradien er 0,8mm.

Man tenke seg at det mangler et komma mellom dem; f.eks. så er 24 2,4mm radius.

For sirkulære skjær der IC = neseradius, designeres dette med 00 hvis størrelsen er konvertert fra tommer og M0 dersom verdien på størrelsen er metrisk.

Den første valgfrie bokstaven, posisjon 8, definerer hvordan eggen er formet og hvordan den er behandlet. Om den er slipt, honet, lakkert, sintret, eller på annen måte bearbeidet.

Men det representerer først og fremst formen på eggen.

Bokstaven i posisjon 9 representerer hvilken hånd eller retning skjæret er ment til å bevege seg i.

 

Posisjon 10 definerer ytterligere formen på eggen dersom skjæret ikke har en enkel tupp med neseradius:

Dette oppgis hovedsakelig dersom posisjon 7 er bokstaver, og slike skjær har vanligvis skrå og skarpe kanter (ingen hjørneradier).

Tabeller hentet fra Mitsubishi Carbide. すみません

Bløtlodding av frontsikte

/

Å feste et frontsikte på et løp gjøres vel kanskje mindre å mindre disse dager, ettersom jeg har inntrykk av at det foretrekkes å ikke ha noe skur og korn dersom et en ny pipe settes i, men heller bare bruke optiske siktemidler. Men det er allikevel noe vi må kunne og dette skulle bløtloddes fast.

Bløtlodding er en prosess der to eller flere materialer (vanligvis metall) sammenføyes med et fyllmateriale, der dette materialet har er lavere smeltepunkt enn delene som skal sammenføyes. Dette fyllmaterialet er som oftest loddetinn. Bløtlodding foregår hovedsakelig under 450 °C, i motsetning til varm-lodding som foregår hovedsakelig over 450 °C.

Disse formene for sammenføyning bruker kapillæreffekten til å trenge inn i alle kriker og kroker mellom delene som sammenføyes og sørger for en god og solid kobling. Kapillæreffekten gir lett-flytende væsker evnen til å stige eller følge trange og tynne passasjer tilsynelatende på tross av eksterne krefter, som f.eks. tyngdekraften.

Jeg fant et løp med et frontsikte vi hadde liggende og varmet opp frontsiktet for å ta det av slik at jeg kunne sette det på igjen. Frontsiktet og løpet ble pusset og renset med smergel. Deretter ble begge deler smurt med en blanding av loddetinn og flussmiddel. Det er selvsagt viktig at flatene passer mot hverandre, og i dette tilfellet var jeg heldig og jobbet med flater som allerede var tilpasset hverandre, men dersom nye ujusterte deler brukes må radiene tilpasses ved sliping eller maskinering. En kurant måte å tilpasse disse delene på ville vært å legge et lag med sandpapir rundt løpet og brukt det til å slipe siktet.

Delene ble varmet opp hver for seg slik at flussmiddelet/tinnet ble varmet opp og fløt utover delene. Denne prosessen kalles fortinning og klargjør delene for sammenføyning ved å forberede flatene med et rent og tynt lag med tinn. Dette laget er godt festet til sitt respektive underlag (delen) og bidrar til god termisk overføring og binding. Det er viktig at begge flatene er fortinnet ordentlig.

Frontsiktet ble så plassert på løpet etter øyemål og ett lodd ble hengt på det. 

Dette loddet har to oppgaver; det ene er å holde siktet fast og gi motstand til å flytte på seg som gjør det enklere å finjustere plasseringen, den andre er å presse det ned på løpet slik at kontaktflatene blir så korrekt som mulig når tinnet smelter.

Siktet og løpet ble varmet opp med en liten propanbrenner, løpet mer enn siktet siden det er større og dissiperer mer varme. Ekstra loddetinn fra rull ble tilført der det trengtes eller så ut som det manglet.

Løpet ble satt til å kjøle seg ned og da det var kaldt begynte jeg å rense opp overflødig loddetinn og pusse sidene blanke igjen.

Loddetinnet i sømmen ble skrapt vekk, det skal være så lite synlig tinn igjen som overhode mulig.

Det ser ikke videre vakkert ut siden delene jeg jobbet med har nok blitt utsatt for dette mange ganger før. Det er ikke dette frontsiktets første rodeo.

Men selve loddingen ble akseptabel. Varmearbeid er fascinerende og jeg lærte mye av en liten oppgave.

Kuledreier? Kule greier!

/

Denne uken, blandt mye annet, har jeg endelig blitt ferdig med et prosjekt jeg har holdt på med lengre enn jeg tør å innrømme. Ikke nødvendigvis fordi jeg jobber tregt, men jeg har ventet på nødvendige deler. Men nå er dingsebomsen endelig ferdig og jeg kan fortelle litt om den.

Jeg har laget en kuledreier! Det er et verktøy for å dreie sfærer i dreiebenken.

Jeg startet opprinnelig med å lage den for å lage en hevarmskule:

Bolt-n.jpg

Med tanke på hvor lang tid jeg har brukt på den hadde det definitivt vært mer effektivt å bare lage hevarmen på den gamle måten med frihånds-dreing og fil, men jeg har lært utrolig mye i løpet av produksjonen og verktøyet ble ypperlig som vi får se senere.

Verktøyet består av to store sirkulære deler som roterer på hverandre, sammenknyttet med en M12 bolt med forsenkningshode. Bolten har en sikringsmutter under, inni basen, for å sørge for at den ikke løsner under bruk.

På den øvre delen av basen sitter dreieskjæret i verktøytårnet. Skjærene er festet til en settherdet ståldel som sørger for stabilitet og mothold for skjæret når det møter arbeidsstykket. Denne er så skrudd i verktøytårnet. Skjærene er TCMT 110204 festet med M2,5 torx insert-skruer. Disse spesifikke skruene var hovedsaklig det jeg måtte vente en stund på før jeg kunne få tatt i bruk verktøyet.

Mer om skjær i et fremtidig innlegg.

Verktøytårnet er festet til svalehale-sleiden med to forsenkede M8 bolter.

Sleiden kan beveges frem og tilbake i dette sporet og kan låses fast i ønsket posisjon ved å stramme de fire set-skruene som dytter på den ene sleidekanten.

Hele verktøyet festes i T-sporet i tverrsleiden på dreiebenken med disse to T-spor mutterne her:

Disse blir så strammet av to M8 bolter som er forsenket inn i basen og den øvre delen må vris til riktig posisjon for å få tilgang til boltene.

Den er altså festet slik:

Spaken bak brukes for å vri den rundt arbeidsstykket og dette skaper kuleformen.

Det eneste som nå manglet var et godt grep på denne spaken, så kronen på verket var å lage en messingkule til enden av spaken med verktøyet. På den måten har verktøyet fullført seg selv!

Her er noen videoer av den i aksjon:

Det ferdige resultatet:

 

Hevarmen

Så var den virkelige testen kommet. Å dreie stål; å lage den hevarmen som jeg i utgangspunktet lagde dette verktøyet for.

Jeg fikk en tegning på hvordan hevarmen skulle være. En klassisk hevarm har en litt dråpeformet kule, men siden jeg benyttet kuledreiern min fikk jeg lage en litt mer sfærisk hevarmskule.

Det viktigste å tenke på med dette verktøyet når man skal lage sfærer er at senter av basen, altså det punktet verktøyet roterer om, er rett under og i senter av den kulen som skal dreies. Ved å sette senter utenfor eller forbi midten av kulen kan man lage ovale former og lignende.

Verktøyet har også skjær utvendig for å lage konkave former.

For å bruke verktøyet setter man først skjæret til senter av basen. På bildet under kan man så vidt se to rissede punkter som representerer at tuppen av det innerste skjæret er i senter av basen. Dette er en av de få pirketingene jeg gjerne skulle funnet en finere løsning for, kanskje lodde fast en bit av en linjal, eller på en eller annen måte gravere inn en millimeter-skala, men det er ikke nødvendig og funker helt fint uten.

Deretter kjøres verktøyet inntil arbeidsstykket til det så vidt møtes, og den digitale avleseren på dreiebenken nulles. Det er her viktig at vektøyet står mer eller mindre 90° på arbeidsstykket. Når avleseren er nullet kan tverrsleiden kjøres inn radien av arbeidsstykket (eller diameteren om avleseren er satt til diameter-modus, som de vanligvis er) mens vektøyet blir presset mot arbeidsstykket og da blir dyttet bakover i sleiden og vil innta den nøyaktige radius som arbeidsstykket har. Det er her selvsagt viktig at arbeidsstykket er dreiet ned til ønsket radius på kulen på forhånd.

Verktøyet føres tilbake ut fra arbeidsstykket og låses fast. Det vil da være kalibrert til korrekt radius.

For å begynne å dreie kulen settes en av aksene, X (radial / diameter) eller Z (aksial / lengde) til null, det spiller liten rolle hvilken.

Deretter avanseres kuttet med den andre aksen mens man roterer verktøyet. Etterhvert som man nærmer seg nullpunket for begge akser vil en kule eller halvkule fremarte seg. 

Deretter gjenstod det litt dreiing for å tynne ned selve armen og litt lett filing og pussing.

Den skulle også varmbøyes ca. 30°. Her brukte jeg nok litt for direkte og hard varme og litt mye oksygen i blandingen med acetylenen for det ble brent opp litt stål i bøyepunktet.

Det var ganske mye gods å varme opp, men det gikk nå til slutt og skadene er ikke noe litt smergel ikke kan fikse.

All done! Denne oppgaven tok både et halvt år og én time. Snodig det. Men verktøyet fungerte nydelig og jeg har lært mye av å lage det og hevarmen i seg selv ble ypperlig.

Tilvirkning av toarmet bladfjær

/

Etter all den fysikken jeg nettopp kjempet meg gjennom kan vi ta alt det og kaste det til siden fordi denne obligatoriske oppgaven ikke krever noe av det. Jeg skulle lage en kopi av en fjær vi hadde og så lenge materialet er det samme og bearbeidingen nogenlunde lik burde resultatet bli korrekt.

En toarmet bladfjær er som navnet tilsier et stykke fjærstål som bøyer seg, sammensatt av to armer. Fordelen med bladfjærer er at de kan ha former som egner seg godt i våpen og andre steder hvor man trenger retningsbestemte krefter og det ikke er plass til en kompresjonsfjær. 

I disse spesifikke bladfjærene som har seksjoner som fjærer mot hverandre mellom et felles punkt er det lengden på armene og tykkelsen på materialet som bestemmer fjæringkraften. De er ikke laget av sylindrisk tråd og kan ha et relativt stort tverrsnitt i forhold til tradisjonelle fjærer og kan derfor bære mye last, men de kan i likhet med heliksfjærer ikke sprike alt for mye ettersom det vil føre til at fjærens solide posisjon (full kompresjon) vil overstige materialets plastiske grense.

Fjæren jeg skulle lage var en slagfjær (fjæren som driver slagsystemet) til en Sauer mod. 8 sideligger.

Jeg begynte med å kappe et passende stykke fjærstål, langt nok til begge armene, og bøyde det. I dette tilfellet tror jeg det ble brukt Nablo 1248 Fjærstål. Ståltyper og destigneringer er et kapittel for seg selv, men dette tallet kalles Engineering Number (EN) og det første tallet indikerer legeringstypen: 1XXX betyr at det er vanlig, rent karbonstål. X2XX betyr at stålet er tilført svovel og fosfor for å gjøre det lettere å maskinere. De to siste XX48 betyr at stålet inneholder 0,48% karbon, typisk for et mildt fjærstål.

Jeg bøyde det ved å varme opp midten med oxy-acetylen brenneren og hamre den flatt sammen. Det er her viktig å passe på at man brenner med en ren flamme, for mye acetylen kan tilføre karbon i stålet og gjøre bøyepunktet sprøere, for mye oksygen kan oksidere stålet slik at det blir spist opp. Men det er et tema for en annen gang.

Deretter satte jeg opp den bøyde biten med fjærstål i fresen og med et hardmetallskjær freste jeg ned tykkelsen på fjæren ned til ca 0,5mm over den eksakte tykkelsen. Resten kunne jeg ta med fil senere, bedre å ha litt ekstra å jobbe med enn litt for lite, spesielt siden jeg måtte rense opp den andre siden også, som jeg også gjorde i fresen, men kun et veldig lett kutt.

Jeg renset opp alle de tilgjengelige sidene etter varmebehandlingen som også hadde etterlatt glødeskall i bøyepunktet. Jeg begynte nå å file fjæren til formen etter modellen vi skulle kopiere. Men før jeg gjorde det glødet jeg ut biten slik at filingen skulle gå lettere.

Når vi varmer opp stålet til det gløder og det kjøler seg ned igjen relativt raskt (ligge i romtemperatur) så herder det littegrann og dette førte til at stålet i bøyepunktet er litt mer motstandsdyktig ovenfor filen enn resten av fjæren. Dette gjør det problematisk å file siden filen ikke tar like mye over det hele og vil innføre bølger og ujevnheter i fjæren. Ved å 'gløde ut' stålet avslapper vi det tilbake til sin mykere tilstand som gjør det mye lettere å bearbeide. Å gløde ut, som på sett og vis er en lokal normalisering, gjøres ved å legge stålet i en ovn og varme det opp til ca 700°C, men dette varierer litt fra kilde til kilde og stål til stål, men ihvertfall ikke langt unna herdetemperatur (ca 800°C). Det skal i hvertfall gløde som navnet tilsier.

Vi har en ovn som er programmerbar med flere stadier dersom noe skulle trenge en spesiell varmebehandling. På kontrollpanelet tilsvarer T1-T4 de fire stadiene. Man trenger ikke bruke alle hvis det ikke er nødvendig. Knappene langs X-aksen er tidsinnstillinger for hvert stadie. Den første knappen styrer start-tidspunktet slik at ovnen kan settes til å vente så å så lenge før den varmer seg opp, for eksempel slik at den er varm når man kommer på skolen dagen etterpå. De etterfølgende knappene styrer hvor lang tid ovnen bruker på å varme seg opp til neste stadie og hvor lenge den skal holde seg på det stadiet. Dette kan sees på grafen som de stigende og de horisontale delene respektivt.

For å gløde ut fjæren trenges det kun å bruke ett stadie der ovnen varmer seg opp til rett temperatur og deretter slår seg av. Den håpefulle fjæren blir liggende i ovnen og ri den saktegående nedkjølingen sammen med ovnen. Den kan tas ut litt før om ønskelig, ved ca 400°C ettersom den viktigste delen av avslappingen nå er over. Hele fjæren er nå tilbake til samme mykhet over det hele.

 

Etter at grovformingen var utført var det på tide å bøye den litt igjen; få den nærmere sitt endelige utseende og gjøre det enklere å fullføre formingen.

Disse bladfjærene er formet med en lett bøy i seg for å bøye seg finere/rettere og utnytte mer av fjæringspotensialet. De har også en gradvis avtagning mot tuppene, dette for å bøye seg sammen rett og fint uten av noen del av de to armene berører hverandre før fjæren er helt komprimert.

I illustrasjonen over vil den øverste fjæren ha en bule på midten i punkt A fordi armene er rette. I forhold til påkjenningen der armene møtes er kreftene relativt små ytterst på armene, men de er lenger fra senter og har dermed lettere for å bøye seg. Siden dette ikke er kompensert for med en bøy i armene vil de bule ut.

I den midterste illustrasjonen er dette kompensert for, men dersom armene er like tykke hele veien vil de innerste delen av armene, som nå er mye nærmere hverandre i forhold til tuppene, treffe hverandre i punkt B før hele kompresjonen er fullført som vil flytte vippepunktet og føre til ujevn fjæring.

I den nederste illustrasjonen er dette også kompensert for ved å tynne tuppene av armene med en gradvis overgang mot møtepunktet. Denne formen vil gi jevn fjæring og en rett og fin lukking av fjæren; mye gods innerst som sørger for god og høy belastningsevne og graderte armer som sikrer en tilnærmet lineær sammenlukking og jevn fordeling av kreftene gjennom fjæringen.

 

Trikset for å få en fin bøy er å dytte eller dra tuppen av armen utover og varme opp hele armen for deretter å bruke brenneren ytterligere til å bøye mer spesifikt, varme opp litt mer der det trengs litt mer bøy.

I bildet under er jeg nesten ferdig med bøyingen, jeg måtte bare bøye litt ekstra inne ved roten av armen.

Jeg bøyde fjæren til litt over slik modellen var, for jeg ble fortalt at den ville 'sette seg' ca 10%, som jeg antar er at full kompresjon overstiger den elastiske grensen til materialet og etter dekompresjon vil legge seg til ro ytterst på denne grensen. Om dette er noe som hadde skjedd uavhengig av avstanden mellom armene eller et annet aspekt av designet til fjæren, eller om det gjelder kun disse fjærene fordi de er designet til å overstige den elastiske grensen er jeg ikke sikker på, men jeg la ihvertfall inn 10% overmål mellom armene. På modellen var det rundt 20mm fra tupp til tupp og jeg bøyde min dermed til å bli ca 22mm.

Dermed var det finformingen igjen. Fjæren var igjen blitt relativt hard, så nålfiler og smergel kom til god nytte her.

Deretter var det tilbake i ovnen for å herde ved 850°C i 5 min for så å bråkjøle i olje. Olje gir en litt snillere og mindre brutal herding enn vann.

Etterfulgt av en anløping ved 360°C i 20 min.

Så ble den pusset fin og blank igjen og var klar for testing og inspeksjon:

En grunnleggende belastningstest for å påse at den tålte det den skulle tåle. Dette viste også om den lukket seg rett og fint. Det gjorde den, men graderingen av armene kunne vært litt bedre.

Deretter den virkelige testen. Fjæren ble plassert i våpenet den var designet for:

Her ser vi baskylen som den sitter i. Test av slagsystem i en hagle kan gjøres ved å plassere en ti-kroning der patronen skulle hvilt og avfyrt. Dersom mynten flyr i taket er testen bestått. Som vi kan se har Kong Harald fått seg en fin liten øredobb, så fjæren bestod testen med glans.

Dette var første gangen jeg arbeidet med fjærstål på en slik måte og jeg må si det var en veldig interessant og innsiktsrik oppgave. Jeg lærte mye om både varmebehandling og ståltyper i prosessen og det å ha lagd noe som faktisk kan selges føles veldig godt.

Spring Theory

/

Fjærer er et meget utbredt og viktig mekanisk element som bidrar til at nesten alt vi bruker til daglig skal fungere. Det er vanskelig å peke på noe mekanisk som ikke inneholder en eller flere fjærer av et eller annet slag.

Fjærer finnes i et uendelig utvalg utførelser og er ofte spesialdesignet til formålet. Man får kjøpt sett med standard størrelser og krefter, men ofte i dyrere og mer avanserte innretninger må fjærer beregnes, designes og produseres etter unike spesifikasjoner.

En fjær er en mekanisk innretning som lagrer mekaniske krefter i form av potensiell energi. De er som oftest laget av fjærstål, som er et høy-kvalitets stål med et høyere karboninnhold (mellom 0,4% - 1,05%) enn vanlig maskinstål (mellom 0,05% - 0,3%) , samt høyere verdier av andre varierende grunnstoffer som mangan, svovel, fosfor, silikon, krom og nikkel. Fjærer kan også være laget av andre ting som plast, gummi, tre eller lignende. En bue er for eksempel i bunn og grunn en stor bladfjær av tre.

 

Typer fjærer

Fjærer kommer som sagt i mange utførelser og varianter, men de vanligste former og bruksområder er som følger:

mechanical-spring-250x250.jpeg

Kompresjonsfjær

Kompresjonsfjærer er kanskje den vanligste typen mekanisk fjær og er antakeligvis den formen man tenker på når man tenker på en fjær. De er ofte laget av ståltråd som er viklet i en heliks med godt mellomrom mellom viklingene og flate ender. Disse lagrer energi når de blir komprimert i den aksiale rettningen. Brukes i alt mellom himmel og jord der noe må dyttes eller holdes fra hverandre eller på plass, men fortsatt kunne bevege seg.

extension977f4ba23a9043daaeae2e5816b3adfe.png

Ekspansjonsfjær / Trekkfjær

Ekspansjonsfjærer er også ekstremt vanlige og fungerer på samme måte som komresjonsfjærer, bare motsatt. De er ofte laget på samme måte som kompresjonsfjærer, men viklingene ligger tett inntil hverandre og endene har ofte kroker til å hekte i det som skal trekkes sammen. Disse lagrer energi når de blir trukket fra hverandre og avstanden mellom viklingene øker. Brukes også overalt, men ofte i dører og andre ting som skal være trukket sammen i normal tilstand.

 

21b5pprx6xL.jpg

Torsjonsfjær

Torsjonsfjærer er enda en veldig vanlig type fjær, men den fungerer på en annen måte enn de to overstående typene. I stedet for å lagre energi ved å endre lengde aksialt, bygges energien opp ved å bøye viklingene radialt, eller vinkelrett fra aksen, rundt aksen. De er laget mye på samme måte som ekspansjonsfjærer, men hakene er strukket rett ut tangentielt fra fjæren. Brukes ofte på samme måte som kompresjonsfjærer, men der det ikke er plass til å ha en slik vinkelrett på flaten som skal dyttes. Brukes f.eks. i klesklyper.

single-spiral-torsion.jpg

Spiralfjær

Spiralfjærer er, som navnet tilsier, viklet i en spiral og lagrer energien ved å slange seg rundt seg selv og vil bli mindre i diameter. En spiralfjær har ganske lang arbeidslengde siden den strammes rundt seg selv og kan trekkes flere ganger rundt. De har ofte et fast punkt i midten hvor de er festet til et statisk punkt i maskinen og den yttre haken driver noe rundt i sirkel. Brukes mye i urverk.

 

 

volute-spring-250x250.jpg

Volutt fjær

Volutte fjærer er på en måte en blanding av spiralfjærer og kompresjonsfjærer i det at viklingene overlapper hverandre i en spiral mens det dannes en konisk heliks av båndet. Disse fjærene har høy belastningsevne og er selvrettende, d.v.s. de bøyer seg ikke like mye ut til sidene dersom de blir belastet uten ekstern støtte som f.eks. ekspansjonsfjærer av viklet tråd. De kan derfor brukes alene uten støtte. Disse ser man brukt på tenger og annet verktøy.

BellevilleSprings2-n.gif

Belleville-fjær

Belleville-fjærer er flere belleville-skiver stablet oppå hverandre til å skape en økt fjærende funksjon og øke arbeidslengden. En belleville-skive er en skive som er bøyd til en konisk form og brukes som låseskiver på bolter for å skape økt motpress på bolten. Flere av disse vil som sagt danne en belleville-fjær. De har begrenset arbeidslengde, men tåler høy last.

De kan stables i serie eller parallel. I serie stables de motsatt om hverandre slike at tuppene møtes innerst og ytterst om hverandre. I parallel legges de samme vei flere av gangen. Serie vil øke arbeidslengden, mens parallel vil øke kraften som trengs for å komprimere den.

Det er en veldig modulær form for fjær, men trenger støtte enten i midten eller på utsiden for å fungere.

single-turn-wave-spring-n.jpg

Bølgefjær

Bølgefjærer er en form for kompresjonsfjærer med noen fordeler. De er kveilet med flatt stålbånd som blir bølget, og det er disse bølgene som skaper den fjærende effekten. Evnene til en bølgefjær kan endres ved å endre tykkelsen og bredden på båndet, antall bølger, høyden på bølgene og antall viklinger. Blandt fordelene denne gir er at arbeidslengden kan mer eller mindre halveres mens kraften forblir den samme sammenlignet med tradisjonelle tråd-fjærer.

Small-flat-spring.jpg

Bladfjær

Når vi sier bladfjær tenker nok mange på de store fjæringssystemene på biler og vogner og slikt, men som børsemakerelev har ordet en litt annen betydning for meg.

1353140.jpg

En bladfjær er i bunn og grunn den enkleste formen for fjær; en flat bit med rett, vinklet eller bøyd stål. En bladfjær har vanligvis ikke gjentagende former (med mindre det er en trekkspillfjær) i motsetning til alle andre tidligere nevnte fjærtyper. Brukes overalt, du har helt sikkert en av plastik på kulepennen din.

 

<-- Magasinfjær (trekkspillfjær, som er en form for bladfjær)

 

 

 

 

 

 

Det finnes mange andre typer og former av fjærer, mange flere enn jeg kan ramse opp, men andre fjærer som kan være vanlig å støte på er stort sett varianter av kompresjonsfjærer og andre heliks-fjærer som dette:

Ikke-lineære fjærer er interessante fordi ved å endre avstanden mellom viklingene kan man endre hvordan fjæren oppfører seg og dermed oppnå en fjæring som ikke er konstant over hele fjærens arbeidslengde. Alle fjærene i bildet over er teknisk sett ikke-lineære, dog begrepet brukes hovedsaklig om fjærer med konstant diameter, men ulik viklingsavstand:

2016-02-15_01-16-31-n.jpg

Det finnes også nestede fjærer, som er en fjær med en fjær inni seg. Disse er viklet motsatt vei for å hindre at de to fjærene hekter seg opp i hverandre. Disse brukes hvis én fjær ikke er nok og det ikke er plass til en større fjær, eller som backup hvis hovedfjæren skulle ryke. De kan også drive forskjellige ting på samme akse.

 

 

 

Fjærens anatomi

Parametriske verdier:

  • D = Fjærens effektive diameter, kan finnes ved å bruke formlene til høyre -->

  • d = Trådens diameter

  • Di = Interne diameter

  • De = Eksterne diameter

 

  • L0 = Total lengde

  • Lr = Arbeidslengde, den lengden fjæren "fjærer" på

  • Lc eller Ls = Solid lengde, fjæren kan ikke komprimeres forbi dette punktet (med unntak)

 

  • P = Viklingsavtand (pitch)

  • α = Heliksvinkel, målt i fjærens frilengde, vil endre seg ettersom fjæren blir komprimert.

 

  • nt = Totalt antall viklinger

  • n eller na = Aktive viklinger

  • ne = Endeviklinger

 

  • Endeutførelse er måten endene på fjæren er bearbeidet på og vil påvirke hvordan aktive viklinger telles:

Måter å finne fjærens diameter på.

Måter å finne fjærens diameter på.

Det er viktig å påpeke at én vikling av en fjær med de samme karakteristikken som en lenger fjær tåler akkurat like mye last, det eneste vi oppnår med flere viklinger er å spre lasten ut over en lengre distanse slik at vi får en lengre arbeidslengde.

 

Fjærindeks C

D og d brukes igjen til å regne ut C som representerer fjærindeksen:

spring_index.png

f.eks. vil en fjær med effektiv diameter 12mm og en trådtykkelse på 1,5mm ha en indeks på 8. En fjær på 16mm med 2mm tykk tråd vil ha samme indeks. Indeksen representerer formen og egenskapene til fjæren. De fleste kompresjonsfjærer har en indeks fra 6 til 12.

Fjærer med indeks 4 eller under er små med tykk tråd og er vanskelig å produsere fordi tråden må bøyes veldig kraftig og kreftene på verktøyet er store. En indeks på 1 vil si at fjærens interne diameter er lik 0.

Fjærer med indeks 25 eller mer er store med tynn tråd og er også komplisert å produsere til eksakte mål. De er vanskelig å ha med å gjøre siden de oppfører seg som trappetroll og har generelt sett ingen praktisk verdi. Veldig store verdier for C vil ende opp med at fjæren kollapser under sin egen vekt på grunn av den forholdsvis tynne tråden.

Fjærindeksen brukes for å regne ut en del andre verdier for en gitt fjær.

 

Hookes Lov

Hookes Lov, oppkalt etter 1600-talls fysiker Robert Hooke, sier at kraften en konvensjonell fjær utøver er proporsjonal med endringen i lengde og uttrykkes slik:

hookes_lov.png

Der F er den kraften i Newton som dytter mot det som komprimerer fjæren, hvilket også er årsaken til minustegnet foran k som representerer at det er den gjenopprettende kraften til fjæren, den beskriver altså bare retningen til kraften. X er endringen i lengde i meter, altså distansen fjæren har beveget seg fra den opprinnelige frilengden. k er et forhold (eng: spring rate / spring constant) som avhenger av fjæren; trådtykkelse, viklingsavstand, diameter, materialtype, etc. k kan finnes ved å fysisk måle avstanden en fjær beveger seg når den blir utsatt for en kraft. k = F/X som oppgis i N/m eller Newton per meter (ikke Newtonmeter (Nm)). Dette forholdet kan også oppgis som R for 'rate'. Hookes lov beskriver en ideell fjær, men er en god tilnærming til de fleste ekte fjærer. En annen måte å si det på er at; motpresset i et objekt er lik den påførte belastningen innenfor det elastiske området til objektet.

Hvis vi vet dette forholdet k kan vi regne ut hvor mye kraft fjæren utøver ettersom hvor sammenklemt eller utstrukket den er. Dette fordrer selvsagt at all denne endringen i lengde foregår innenfor fjærens elastiske grenser: 

Den midterste fjæren i bildet til høyre representerer fjæren i avslappet tilstand. X-aksen viser endring i lengde mens Y-aksen viser påført belastning.

Ettersom den blir komprimert vil X synke proporsjonalt med belastningen helt til fjæren når sin solide form og vil ikke kunne komprimeres ytterligere; som vises på grafen der belastningen øker, men komprimeringen avtar.

Når fjæren trekkes ut gjelder også Hookes lov som er representert av den røde linjen. Den stiplede grå streken viser hvordan fjæren oppfører seg i virkeligheten. Vi kan se at etterhvert som vi drar fjæren ut over dens elastiske grense vil den begynne å deformere seg helt til den er trukket helt rett ut og vi vil se den samme økningen i belastning mens endringen i lengde avtar opp til det punktet at tråden ryker.

Image14-n.gif

Torsjonsfjærer følger en angulær form for Hookes lov:

torsional_hookes_law.png

Der:

  • τ (tau) = Det påførte momentet i Newtonmeter

  • k = Fjæringskonstanten

  • θ (theta) = Vridningen av fjæren fra hvileposisjonen i radianer, mer om radianer her

 

Elastisk og plastisk deformasjon og Youngs modulus

Plastisk og elastisk deformasjon er viktige begreper innen fjæring, men gjelder så godt som alle materialer. Belastning (stress) og påkjenning (strain) [eller motpress eller deformering] er verdier som brukes for å beskrive defleksjon, eller hvor mye et materiale er tilbøyelig til å endre seg dimensjonalt under så og så mye påført kraft, og kurven som brukes for å beskrive disse verdiene definerer også ofte punktet der materialet vil bli påført permanente endringer og når det brekker.

Elastisk deformasjon er når materialet blir påført kraft slik at det bøyer seg og deretter returnerer til sin opprinnelige form når belastningen blir fjernet.

Plastisk deformasjon forekommer når materialet blir bøyd over dette punktet og all bøying etter dette blir permanent endring når belastningen opphører.

Belastningen kan måles og oppgis i Pascal (trykk) eller Newton per kvadratmeter, som er definisjonen på en Pascal, mens påkjenningen (som er et fellesbegrep som varierer fra materiale til materiale og er også et forhold og er dermed dimensjonsløst) måles i graden av endring i materialet i kraftretningen og oppgis vanligvis i meter per meter; men: det er mer korrekt å si at det oppgis i lengde per lengde, siden påkjenningen som sagt er et forhold mellom endringen i lengden på materialet og materialets opprinnelige lengde, og ettersom materialet blir utsatt for økende trykk så vil dette forholdet øke. Vi må bruke et forhold siden selv om egenskapene til materialet vil være likt i ulike tilfeller så vil materialets faktiske mengde / fysiske størrelse påvirke hvordan det oppfører seg. Det er lettere å bøye noe tynt enn noe tykt, men i forhold til tykkelsen vil materialet oppføre seg likt.

Det er her Young's modulus kommer inn i bildet. Oppkalt etter 1800-talls vitenskapsmannen Thomas Young (men konseptet ble oppfunnet av den legendariske Leonhard Euler) og definerer stivheten til materialer. Youngs modulus kalkuleres ved å ta belastningen delt på påkjenningen, som gir enda et forhold: Y. Kan også være E for 'elastic modulus'. Youngs modulus oppgis vanligvis i megaPascal eller gigaPascal, men er også i grunnen dimensjonsløst.

youngs_modulus_formula.png

En lav verdi, f.eks. 0,1 vil si at materialet er veldig fleksibelt og mykt siden 1 enhet belastning tilsvarer 10 enheter påkjenning. Dette vil si f.eks. gummi.

En høy verdi, f.eks. 100 tilsier at materialet krever et trykk på eksempelvis 200 enheter belastning for å endre seg 2 enheter lengde. Som f.eks. glass

metals.jpg

Altså brukes Youngs modulus til å forutsi dimensjonale endringer i materialer under strekk eller press. Det er også viktig å påpeke at Youngs modulus er en lineær funksjon og er brukbar kun innenfor det elastiske området til materialet, altså kan den bare brukes der Hookes lov gjelder.

 

Poissons forhold

Poissons forhold er et forhold som beskriver den tverrgående endringen i tykkelse i et materiale når det blir utsatt for en langsgående påkjenning. Det er strengt tatt ikke nødvendig å bruke ved produksjon av alminnelige fjærer, men det er kjekt å vite om.

Når en stang blir strukket ut må det materialet som gjør at stangen blir lengre komme fra et sted, og det blir da tatt fra tykkelsen. Og motsatt; dersom stangen komprimeres vil diameteren øke. 

ε long står for 'longitudinal' og er endringen i lengderetningen. kan også hete ε axial.

ε lat står for  'latitudinal' og er endringen i diameter. Kan også hete ε trans.

Forholdet uttrykker altså forholdet til endringen i bredde delt på forholdet til endringen i lengde. Minustegnet er der for at forholdet skal ha en positiv verdi ettersom svaret vil bli et negativt tall. Forholdet betegnes med den greske bokstaven 'nu': ν. Blir noen ganger skrevet med 'my'; µ.

De fleste materialer har en verdi mellom 0 og 0,5. Her er en tabell over vanlige materialer og deres Poisson-tall:

Som man kan se av tabellen så har kork en verdi på rundt 0, det vil si at den så godt som ikke opplever tverrgående ekspansjon under aksial kompresjon eller tverrgående sammentrekning under aksialt strekk. Mens gummi har en verdi nærme 0,5 som vil si at den opplever stor endring i tykkelse når det blir sammenpresset eller trukket fra hverandre.

poissons_forhold_enkel formel.png

Så hvis vi trenger å vite hvor mye en tråd krymper i diameter når den blir strukket kan vi bruke en variasjon av formelen slik:

 

poissons_forhold_avansert_formel.png

Formelen over er kun gyldig for små størrelser, dersom større utslag skal kalkuleres bør man benytte denne formelen:

 

 

Poissons forhold er mer komplisert enn dette, spesielt i ikke-sirkulære objekter og det finnes også materialer som ikke følger denne regelen og utvider seg når de blir strukket, men for en grunnleggende forståelse og bruk er formlene over nok. 

 

 

Bruddstyrke og belastningstyper

At vi kan beregne hvor mye et materiale vil bøye eller strekke seg er vel og bra, men det viktigste ved design av fjærer er vel egentlig hvor mye last de tåler før de brekker. Hvis vi kan designe en fjær som leverer det motpresset eller energien vi trenger og vite at den ikke kommer til å brekke under normale belastninger så er jobben vår gjort.

Noen fjærer er ikke designet for å bevege seg i hele arbeidsområdet sitt. Bilfjærer for eksempel har ikke godt av å bli komprimert helt ned til sin solide posisjon. De tåler det sikkert, men de er ikke 'laget' for det.

Det er hovedsakelig tre former for belastning; strekk, trykk og skjær. 

Strekk- og trykkbelastning er krefter der påkjenningen og det eventuelle bruddet forekommer vinkelrett på kraftretningen, mens ved skjærende belastning blir påkjenningen parallell med kraftretningen. 

På engelsk heter dette henholdsvis 'tensile stress', 'compressive stress' og 'shear stress'. 

Mechanical+Properties-n.jpg

Her er en vikling av en fjær. Fjæren i sin helhet blir selvsagt utsatt for strekk- eller trykkbelastning, men inne i fjæren er det noe annet som fører til den fjærende effekten.

Når A og B trekkes fra hverandre eller dyttes mot hverandre vil det forårsake vridning i punkt C. Vridning i et materiale, eller torsjonal belastning er en form for skjærbelastning.

Generell skjærbelastning er en funksjon av kraften over arealet av tverrsnittet:

generelt_shear_stress.png

Generell skjærbelastnig betegnes med den greske bokstaven 'tau' τ.

Ren skjærbelastning i f.eks. en stang som vris kan finnes ved:

pure_shear_stress.png

  • γ (gamma) = Påkjenningen

  • G = Belastningsmodulusen til materialet (shear modulus / torsional modulus of elasticity)

γ kan vi finne slik:

shear_strain.png

  • ρ (rho) = En avstand fra senter av sylinderen i meter, vanligvis c

  • φ (phi) = Vinkelen på vridning i radianer, betegnes også noen ganger med θ (theta)

  • L = Lengden på det vridde elementet i meter

  • c = Radien til sylinderen i meter

  • T = Det påførte momentet i Newtonmeter (Nm)

Torsjonspåkjenningen er altså et resultat av vridningen over en avstand av materialet. Påkjenningen øker proporsjonalt med avstanden fra senter, det er minst påkjenning i midten av sylinderen og mest ved omkretsen der endringen er størst. Dersom man vil finne påkjenningen et sted langs radien endrer man ρ til noe annet enn c, som foreksempel c/2 som finner påkjenningen halvveis mellom senter og omkretsen.

Skjærbelastnings-modulusen G finner vi av følgende formel:

belastningsmodulus.png

Her ser vi at modulusen avhenger av både Youngs modulus og Poissons forhold. Det er også resultatet av den skjærbelastningen delt på den torsjonale påkjenningen.

 

Praktiske formler

For å regne ut diverse egenskaper til fjærer med de fysiske data vi har tilgjengelig finnes noen praktiske formler:

Fjæringskonstanten k kan finnes fra denne formelen:

spring_rate.png

Maksimal torsjonal belastning for en fjær gis ved: 

max_shear_force.png

  • fs = Maksimal belastning (max shear force)

  • T = Momentet (torque) i Newtonmeter. Momentet er som kjent kraft ganger arm, og i dette tilfellet er kraften den påførte lasten på fjæren i Newton og armen er D/2 siden armen regnes fra senter av fjæren og påvirker begge sider av viklingen likt. Så dette gir:

max_shear_force_expanded.png

Der W er belastnigen i Newton. Så for å finne maksimal last for en gitt tråd før den ryker kan vi snu formelen:

max_load.png

Men det fordrer at vi vet hvor mye torsjonal belastning tråden tåler.

Som vi kan se av disse formlene er lasten en fjær tåler proporsjonal med tykkelsen på tråden og omvendt proporsjonal med diameteren på fjæren. Ved å doble trådtykkelsen blir fjæren 8 ganger så sterk og ved å doble fjærdiameteren blir fjæren halvparten så sterk.

Hvor stor endringen i lengden på fjæren vil være uten å vite fjæringskonstanten kan regnes ut slik:

spring_deflection.png

 

Kurve-effekten og Wahl-faktor

Mange av disse og følgende kalkuleringer går utifra at tråden i fjæren er rett, men det er den jo ikke. Tråden i viklingene bøyer seg naturligvis og dette medfører ekstra former for belastning på tråden τ og fjæringsforholdet k. Materialet i tråden vil strekke seg på utsiden av fjæren og komprimeres på innsiden av fjæren. Dette kalles kurve-effekten og Wahl-faktoren er en verdi K vi modulerer med for å korrigere for denne effekten.

curvature.png

I grafen over er K1 Wahl-faktoren som modulerer belastningsgrensen. Formelen for denne faktoren bruker fjærindeksen C og ser slik ut:

wahl_faktor.png

Denne verdien ganges da med resultatet fra belastningsberegningen slik at vi får:

max_shear_force_expanded_wahl.png

Det finnes en lignende formel som beregner det samme og er kjent som Bergsträsser-faktoren:

bergstrasser_faktor.png

Forskjellen mellom Wahl og Bergsträsser er mindre enn 1% så Bergsträsser er å foretrekke.

K2 korrigerer fjæringskonstanten k:

deflection_factor.png

Slik at vi får:

spring_rate_wahl.png

 

I praksis

Jeg ble interessert i design av fjærer og satte meg inn i det da jeg lagde et viklingsverktøy til dreiebenken. Den mater en tråd opp til 2mm tykk presist rundt en stang som står i kjoksen og ved bruk av maskinmating kan jeg kontrollere viklingsavstanden. 

En bit med stål med et spor i kan presses mot tråden for å øke friksjonen og holde igjen tråden slik at den strammer seg og legger seg godt rundt stangen. Tråden jeg bruker kalles 'pianotråd' eller 'music wire' å kommer ferdig arbeidsherdet fra fabrikken og kan vikles i kald tilstand.

Siden den allerede er herdet og anløpt har den en høy Youngs modulus og vil 'sprette' tilbake til en større fjærdiameter enn det den blir viklet til, så stangen man bruker må være mindre enn den interne fjærdiameteren man ønsker. Det finnes tabeller for dette.

En fjær må ikke lages slik at viklingsavstanden overstiger den plastiske deformasjons-grensen til tråden, ellers vil den aldri tilbakestille seg til opprinnelig lengde etter full kompresjon. Dette kan derimot noen ganger være av design ettersom materialet vil "sette seg".

For andre materialer som ikke er herdet må vi herde fjærene etter at er viklet, disse er også lettere å vikle.

Når vi herder låser vi fast stålet i en konfigurasjon med veldig liten elastisk rekkevidde og kort plastisk deformasjon før det når bruddpunktet, ved å anløpe det avslapper vi stålet nok til å utvide det elastiske området drastisk.