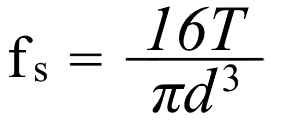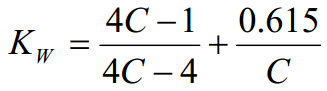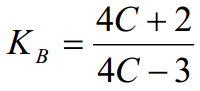Tilvirkning av toarmet bladfjær
/Etter all den fysikken jeg nettopp kjempet meg gjennom kan vi ta alt det og kaste det til siden fordi denne obligatoriske oppgaven ikke krever noe av det. Jeg skulle lage en kopi av en fjær vi hadde og så lenge materialet er det samme og bearbeidingen nogenlunde lik burde resultatet bli korrekt.
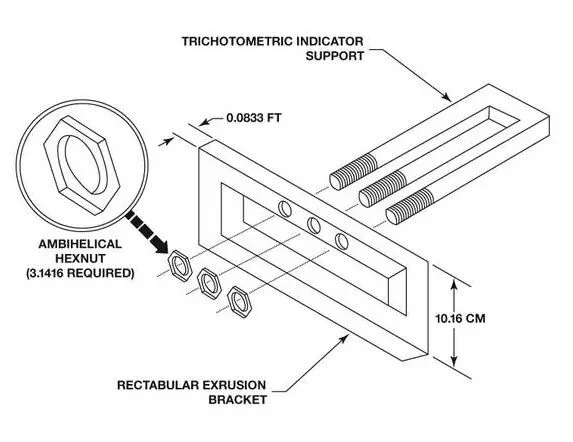
En toarmet bladfjær er som navnet tilsier et stykke fjærstål som bøyer seg, sammensatt av to armer. Fordelen med bladfjærer er at de kan ha former som egner seg godt i våpen og andre steder hvor man trenger retningsbestemte krefter og det ikke er plass til en kompresjonsfjær.
I disse spesifikke bladfjærene som har seksjoner som fjærer mot hverandre mellom et felles punkt er det lengden på armene og tykkelsen på materialet som bestemmer fjæringkraften. De er ikke laget av sylindrisk tråd og kan ha et relativt stort tverrsnitt i forhold til tradisjonelle fjærer og kan derfor bære mye last, men de kan i likhet med heliksfjærer ikke sprike alt for mye ettersom det vil føre til at fjærens solide posisjon (full kompresjon) vil overstige materialets plastiske grense.
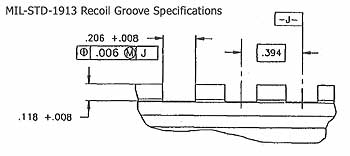
Fjæren jeg skulle lage var en slagfjær (fjæren som driver slagsystemet) til en Sauer mod. 8 sideligger.
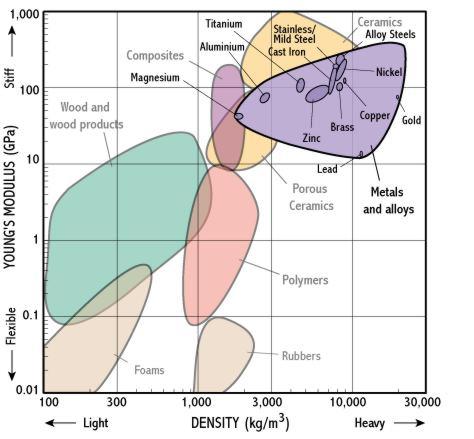
Jeg begynte med å kappe et passende stykke fjærstål, langt nok til begge armene, og bøyde det. I dette tilfellet tror jeg det ble brukt Nablo 1248 Fjærstål. Ståltyper og destigneringer er et kapittel for seg selv, men dette tallet kalles Engineering Number (EN) og det første tallet indikerer legeringstypen: 1XXX betyr at det er vanlig, rent karbonstål. X2XX betyr at stålet er tilført svovel og fosfor for å gjøre det lettere å maskinere. De to siste XX48 betyr at stålet inneholder 0,48% karbon, typisk for et mildt fjærstål.
Jeg bøyde det ved å varme opp midten med oxy-acetylen brenneren og hamre den flatt sammen. Det er her viktig å passe på at man brenner med en ren flamme, for mye acetylen kan tilføre karbon i stålet og gjøre bøyepunktet sprøere, for mye oksygen kan oksidere stålet slik at det blir spist opp. Men det er et tema for en annen gang.
Deretter satte jeg opp den bøyde biten med fjærstål i fresen og med et hardmetallskjær freste jeg ned tykkelsen på fjæren ned til ca 0,5mm over den eksakte tykkelsen. Resten kunne jeg ta med fil senere, bedre å ha litt ekstra å jobbe med enn litt for lite, spesielt siden jeg måtte rense opp den andre siden også, som jeg også gjorde i fresen, men kun et veldig lett kutt.
Jeg renset opp alle de tilgjengelige sidene etter varmebehandlingen som også hadde etterlatt glødeskall i bøyepunktet. Jeg begynte nå å file fjæren til formen etter modellen vi skulle kopiere. Men før jeg gjorde det glødet jeg ut biten slik at filingen skulle gå lettere.
Når vi varmer opp stålet til det gløder og det kjøler seg ned igjen relativt raskt (ligge i romtemperatur) så herder det littegrann og dette førte til at stålet i bøyepunktet er litt mer motstandsdyktig ovenfor filen enn resten av fjæren. Dette gjør det problematisk å file siden filen ikke tar like mye over det hele og vil innføre bølger og ujevnheter i fjæren. Ved å 'gløde ut' stålet avslapper vi det tilbake til sin mykere tilstand som gjør det mye lettere å bearbeide. Å gløde ut, som på sett og vis er en lokal normalisering, gjøres ved å legge stålet i en ovn og varme det opp til ca 700°C, men dette varierer litt fra kilde til kilde og stål til stål, men ihvertfall ikke langt unna herdetemperatur (ca 800°C). Det skal i hvertfall gløde som navnet tilsier.
Vi har en ovn som er programmerbar med flere stadier dersom noe skulle trenge en spesiell varmebehandling. På kontrollpanelet tilsvarer T1-T4 de fire stadiene. Man trenger ikke bruke alle hvis det ikke er nødvendig. Knappene langs X-aksen er tidsinnstillinger for hvert stadie. Den første knappen styrer start-tidspunktet slik at ovnen kan settes til å vente så å så lenge før den varmer seg opp, for eksempel slik at den er varm når man kommer på skolen dagen etterpå. De etterfølgende knappene styrer hvor lang tid ovnen bruker på å varme seg opp til neste stadie og hvor lenge den skal holde seg på det stadiet. Dette kan sees på grafen som de stigende og de horisontale delene respektivt.
For å gløde ut fjæren trenges det kun å bruke ett stadie der ovnen varmer seg opp til rett temperatur og deretter slår seg av. Den håpefulle fjæren blir liggende i ovnen og ri den saktegående nedkjølingen sammen med ovnen. Den kan tas ut litt før om ønskelig, ved ca 400°C ettersom den viktigste delen av avslappingen nå er over. Hele fjæren er nå tilbake til samme mykhet over det hele.
Etter at grovformingen var utført var det på tide å bøye den litt igjen; få den nærmere sitt endelige utseende og gjøre det enklere å fullføre formingen.
Disse bladfjærene er formet med en lett bøy i seg for å bøye seg finere/rettere og utnytte mer av fjæringspotensialet. De har også en gradvis avtagning mot tuppene, dette for å bøye seg sammen rett og fint uten av noen del av de to armene berører hverandre før fjæren er helt komprimert.
I illustrasjonen over vil den øverste fjæren ha en bule på midten i punkt A fordi armene er rette. I forhold til påkjenningen der armene møtes er kreftene relativt små ytterst på armene, men de er lenger fra senter og har dermed lettere for å bøye seg. Siden dette ikke er kompensert for med en bøy i armene vil de bule ut.
I den midterste illustrasjonen er dette kompensert for, men dersom armene er like tykke hele veien vil de innerste delen av armene, som nå er mye nærmere hverandre i forhold til tuppene, treffe hverandre i punkt B før hele kompresjonen er fullført som vil flytte vippepunktet og føre til ujevn fjæring.
I den nederste illustrasjonen er dette også kompensert for ved å tynne tuppene av armene med en gradvis overgang mot møtepunktet. Denne formen vil gi jevn fjæring og en rett og fin lukking av fjæren; mye gods innerst som sørger for god og høy belastningsevne og graderte armer som sikrer en tilnærmet lineær sammenlukking og jevn fordeling av kreftene gjennom fjæringen.
Trikset for å få en fin bøy er å dytte eller dra tuppen av armen utover og varme opp hele armen for deretter å bruke brenneren ytterligere til å bøye mer spesifikt, varme opp litt mer der det trengs litt mer bøy.
I bildet under er jeg nesten ferdig med bøyingen, jeg måtte bare bøye litt ekstra inne ved roten av armen.
Jeg bøyde fjæren til litt over slik modellen var, for jeg ble fortalt at den ville 'sette seg' ca 10%, som jeg antar er at full kompresjon overstiger den elastiske grensen til materialet og etter dekompresjon vil legge seg til ro ytterst på denne grensen. Om dette er noe som hadde skjedd uavhengig av avstanden mellom armene eller et annet aspekt av designet til fjæren, eller om det gjelder kun disse fjærene fordi de er designet til å overstige den elastiske grensen er jeg ikke sikker på, men jeg la ihvertfall inn 10% overmål mellom armene. På modellen var det rundt 20mm fra tupp til tupp og jeg bøyde min dermed til å bli ca 22mm.
Dermed var det finformingen igjen. Fjæren var igjen blitt relativt hard, så nålfiler og smergel kom til god nytte her.
Deretter var det tilbake i ovnen for å herde ved 850°C i 5 min for så å bråkjøle i olje. Olje gir en litt snillere og mindre brutal herding enn vann.
Etterfulgt av en anløping ved 360°C i 20 min.
Så ble den pusset fin og blank igjen og var klar for testing og inspeksjon:
En grunnleggende belastningstest for å påse at den tålte det den skulle tåle. Dette viste også om den lukket seg rett og fint. Det gjorde den, men graderingen av armene kunne vært litt bedre.
Deretter den virkelige testen. Fjæren ble plassert i våpenet den var designet for:
Her ser vi baskylen som den sitter i. Test av slagsystem i en hagle kan gjøres ved å plassere en ti-kroning der patronen skulle hvilt og avfyrt. Dersom mynten flyr i taket er testen bestått. Som vi kan se har Kong Harald fått seg en fin liten øredobb, så fjæren bestod testen med glans.
Dette var første gangen jeg arbeidet med fjærstål på en slik måte og jeg må si det var en veldig interessant og innsiktsrik oppgave. Jeg lærte mye om både varmebehandling og ståltyper i prosessen og det å ha lagd noe som faktisk kan selges føles veldig godt.