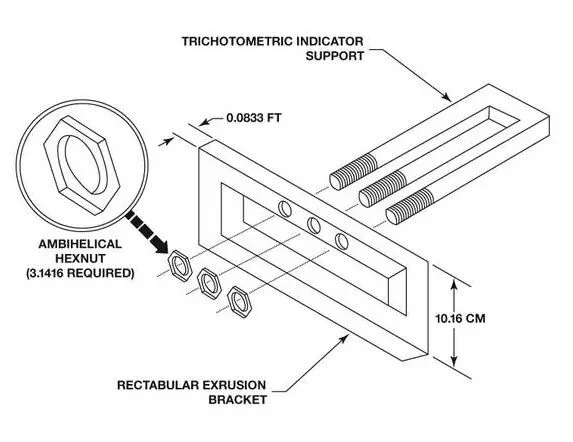
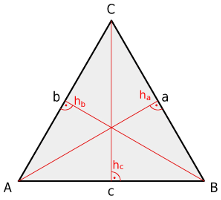
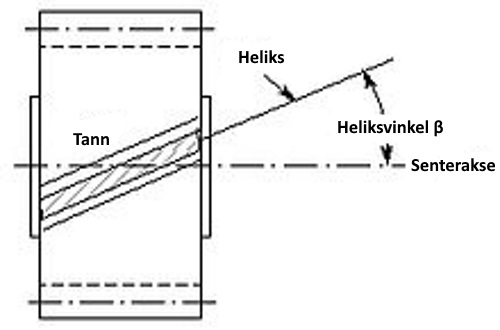
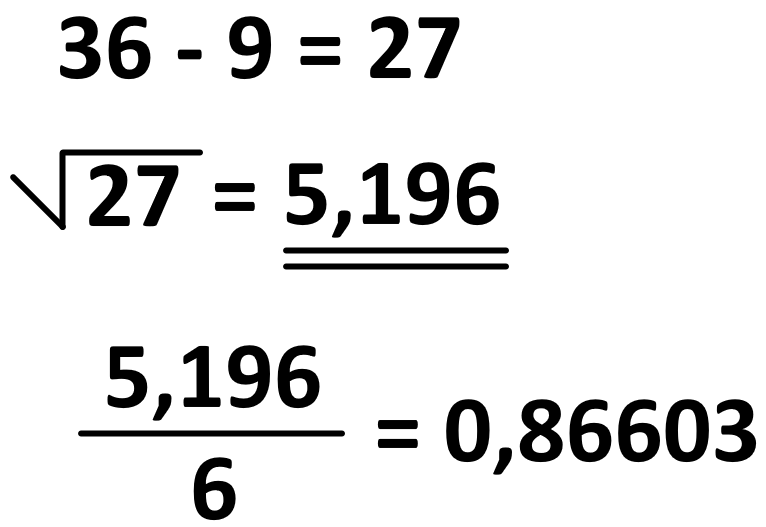Parallellklemme
/Etter å ha holdt på i flere måneder er jeg endelig ferdig med parallellklemmen jeg fikk som ekstraoppgave. Det er flere grunner til at det tok så langtid. For det første var det en omfattende oppgave med mange ulike prosesser, noen som jeg måtte lære meg før jeg kunne fortsette. For det andre så har jeg mye annet å holde på med og det har rett og slett ikke vært nok dager med verksted-tid til å bli ferdig.
Men nå er jeg endelig ferdig og kan fortelle litt om veien dit.
Jeg begynte med et stykke 20x20mm stål som jeg planfreste ned til 18x18mm. Toleransene mine var på 0,1mm, men jeg forsøkte som jeg ofte gjør å se hvor nøyaktig jeg kunne få det.
Jeg spente det opp i stikken og freste den ene siden rett, deretter vred jeg stykket 90° og freste den neste siden. Jeg brukte så disse sidene som referansesider da jeg freste de to andre sidene og dermed hele biten ned til korrekt tykkelse. Jeg var i stand til å oppnå en presisjon på +/- 0,02mm her, og det er jeg ganske fornøyd med.
Planfresen gav ikke en fin overflate, så jeg byttet ut de fem skjærene som viste seg å være ganske slitne og senket matehastigheten til litt over halvparten av det den stod på. Så vidt jeg husker benyttet jeg omdreiningstall på rundt 1000 r/min og matehastighet på ca. 250 mm/min. Dette gav en pen overflatefinhet.
Jeg målte så rettheten og parallelliteten og kom frem til at stykket er litt vridd, men det er innenfor toleranser så det gjør ikke noe. Tall på stykket er hundredeler. Stykket skal uansett deles i to, så da blir ujevnhetene "halvert".
Men før jeg kunne begynne med fresingen jeg gjorde i bildene over måtte jeg reparere fresen, eller rettere sagt det digitale avlesersystemet. Det var i ustand og gav ikke pålitelige utslag.
Skruene til sleide-festet var brukket og avleseren som skal sitte statisk på fresen var løs, samt at sleiden på aksebordet var slarkete, så vi tok av alt, renset det og byttet ut skruene.
Mye bedre.
Deretter kappet jeg arbeidsstykket i to og freste sidene like.
Jeg freste dem her ned til korrekt lengde, dvs. 110mm, med ganske imponerende +/-0,01 mm avvik. I etterpåklokskapens navn hadde det vært en fordel å la det være igjen litt materiale siden endene skulle files runde, men det endte opp med å ikke bli et stort problem.
Da stykkene var innenfor korrekte dimensjoner brukte jeg høyderissemåler, rissepenn, linjal og skyvelære for å risse dato- og reveranselinjer.
Med hovedfreseoperasjonene utført filte jeg endene runde. Jeg grovslipte stykkene med slipemaskin og gjorde resten med flatfil og smergel.
Jeg sjekket ofte med radielære og passet på å holde filen rett. Jeg brukte også filen med smergel i mellom for å få en solid flate mot stykket slik at ikke kantene ble ulikt slitt i forhold til midt på stykket som kan oppstå dersom man bruker smergel for seg selv siden det kan strekke seg.
Deretter kom en litt komplisert operasjon. Andre enden av stykkene skal ha en 22,2° vinkel. Her brukte jeg en ganske nøyaktig vinkelmåler for grovkappet.
Jeg hadde allerede risset referanselinjer, så jeg visste hvor vinkelen skulle starte og stoppe på de to sidene. Da jeg kom nærme målene freste jeg ned til jeg nådde en av de to referanselinjene, enten den på toppen eller den på enden og vinklet stykket litt anderledes. Jeg brukte den siden som var korrekt til å rekalibrere fresehodet og gjorde et kutt for å teste vinkelen. Var det enda litt å gå på banket jeg forsiktig på stykket for å endre vinkelen og rekalibrerte stykket igjen for så å ta et nytt kutt. Det finnes nok en mer eksakt måte å gjøre det på, men vi har ikke skrustikker som kan vinkles i 2 akser, så da måtte jeg gjøre det manuelt. Jeg kunne også vinklet selve fresehodet, noe jeg gjør i en senere operasjon, men det hadde blitt enda mer arbeid å få korrekt vinkel.
Jeg ble ganske fornøyd med resultatet.
Jeg boret hull i stykkene som skruene skal gå gjennom og gjenget disse med M10 gjengtapper.
Her benyttet jeg en pinol/senterspiss for å påse at gjengetappen sto rett. Det fungerte veldig bra.
Når det er sagt så ble ikke hullene helt korrekt overfor hverandre. Jeg hadde stykkene oppå hverandre i stikken i søylebormaskinen slik at hullene skulle bli på nøyaktig samme sted.
Men boringen min var tydeligvis litt ute av senter og jeg hadde dem plassert SAMME VEI slik at når jeg snudde det ene stykket rundt får å skru dem sammen ble feilen åpenbar... Så jeg lagde to nye stykker.
Det var ergerlig å starte så godt som helt på nytt, men jeg kunne ikke leve med slikt slett arbeid hengende over meg.
Denne gangen var jeg ekstra nøye med plasseringen av hullene og jeg boret de to stykkene hver for seg. Da ble det bra.
De vinklede endene skulle files runde med en radius på 5mm. Personlig syns jeg det ser bedre ut som det gjør, men jeg fulgte tegningene.
Det eneste som da gjensto å gjøre med selve klemmene var å frese V-sporet som skal holde klemmen sentrert og gi bedre grep om det som klemmes sammen, samt de skrå sporene på sidene.
For å frese V-sporet brukte jeg en 3mm pinnefres med en collet-kjoks og vinklet fresehodet 45°.
For å vinkle fresehodet løsnet jeg de fire boltene som holder det fast som på bildet under.
Jeg byttet ut fresekjoksen til en collet kjoks. Colleter, eller halser, er utbyttbare kjoksstykker med ulike indre diameter for å sette fast mange typer verktøy eller arbeidsstykker. Når man strammer kjoksen presses colleten sammen og griper og sentrerer verktøyet.
For å bytte collet-holderen skrur vi ut trekkstangen som går gjennom fresehodet ved å skru opp mutteren som strammer den på toppen.
Deretter setter vi inn pinnefresen og strammer med kjoksnøkkelen.
Pinnefresen stakk litt langt ut, men det måtte bli sånn for at kjokshodet skulle gå klar av arbeidsstykket.
V-sporet skulle være 3mm bredt, som vil si at med en 45° vinkel blir kuttet 1,5mm dypt. Jeg freste opp sporene i flere passeringer for ikke å skade pinnefresen siden den var så liten og stakk så langt ut.
På sidene brukte jeg en 4mm pinnefres siden enderadiusen på sporet skulle være 2mm. For å frese disse sidene måtte jeg bruke midten av pinnefresen, som fungerte greit, men ikke optimalt. Hadde jeg hatt V-blokker hadde jeg spent opp stykket anderledes for å kunne heve stykket loddrett opp i fresen i endene for å lage et renere kutt, men etter litt opprensking med fil ble resultatet helt OK.
Skruene var relativt enkle å lage, men det å dreie gjengene var noe jeg måtte lære meg for dette prosjektet og det var en liten utfordring, men det ble gjenger av det til slutt og hvordan har jeg dekket i mitt forrige innlegg.
Jeg dreide så tynne ting at hardmetallskjæret til dreiebenken ikke kunne brukes siden benken ikke går fort nok til å oppnå riktig skjærehastighet. Så jeg slipte mitt eget hurtigstålskjær.
Jeg forsøkte å bruke litt kjølevæske på en mer... manuell måte og resultatet ble forsåvidt greit, men det var ikke verdt bryet, spesielt med tanke på at hodet skal serrateres og resten gjenges.
Jeg serraterte med toppsleiden og meget lav matehastighet med trykkluft som blåste ut sponet. Da ble resultatet meget bedre enn tidligere forsøk.
Jeg slipte et nytt formskjær, 3mm bredt med en radius på 1,5, i hurtigstål for å kutte frisporene til gjengene.
Deretter avfaset jeg endene.
Til slutt dreiet jeg gjengene
Badabing badabom, det tok sin tid, men jeg har lært masse.
Og ikke det at jeg ikke visste dette fra før, men dette prosjektet har virkelig gitt meg viktig lærdom: