Gir og utveksling
/Vet du hvorfor det er så mye olje under havbunnen? Jo for den smører jordaksen. Og hvis vi pumper opp all oljen vil jorda slutte å snurre. Så hvorfor pumper vi opp oljen? Oppfinnelsen av hjulet, som mye av oljen i dag driver rundt, blir betraktet som den første og mest innflytelsesrike oppdagelsen i menneskets historie, og da man lagde dem av metall og puttet tenner på det var tiden inne for maskinalderen.
Tannhjul driver verden fremover med sin trofaste sirkulære og repeterende bevegelse. Ikke-sirkulære tannhjul eksisterer også, men de er brukt i svært spesielle situasjoner. Tannhjul er som navnet tilsier hjul med tenner som overfører mekanisk kraft fra en aksel til en annen.
Utveksling er det som forekommer når ulike tannhjul settes i bruk sammen og driver eller drives rundt. Utveksling er en fundamental teknisk egenskap i maskineri og er grunnen til at vi kan lage maskiner som gjør det de gjør på en effektiv måte. Vi finner utveksling overalt rundt oss, i biler, sykler, kjøkkenmaskiner, verktøy, etc.
Selve grunnprinsippet er relativt enkelt; Et mindre tannhjul som driver et større tannhjul gir mer kraft, men mindre fart. Et større tannhjul som driver et mindre ett gir større fart, men mindre kraft. Partall antall tannhjul gir en endring i retning, mens oddetall antall gir den samme retningen som drivhjulet.
Tannhjul i inngrep er i bunn og grunn konstant roterende eksempler på Newton's tredje lov, om kraft og motkraft.
“Every action has an equal and opposite reaction.”
Jo større tannhjulet er, jo lenger tennene er fra senter, jo lettere er det å snurre det. Kraft ganger arm og alt det der. Derfor er det lettere for et mindre tannhjul å drive et større og omvendt.
Giret som tilfører kraften i systemet blir kalt det drivende hjulet (eng: driver) og det tilkoblede hjulet blir kalt det drevne (eng: driven).
For å få samme rotasjonsretning på det drevne tannhjulet må et ekstra hjul tilføres mellom det drivende og det drevne hjulet. Dette kalles et reverseringshjul (eng: idler gear) fordi det kun eksisterer for endre retningen på det drevne hjulet.
Det går derfor ikke an å sette 3 tannhjul direkte sammen slik som (desverre) ofte blir brukt i logoer som denne:
Her har det gått helt rundt for noen.
Utvekslingsforhold
Utvekslingsforhold (eng: gear ratio) er forholdet mellom tanntallet eller diameteren på to tannhjul og ved reim- eller kjededrift. Utvekslingsforhold uttrykkes på samme måte som målestokk, f.eks. 1:5 (en til fem). Det første tallet representerer det drivende hjulet og det siste representerer det drevne.
Forholdet kan også uttrykkes som brøk 1/2 og 2/1 eller heltall/desimaltall 0,5 eller 2 der tallet representerer hvor mange ganger det drivende hjulet går rundt per revolusjon av det drevne
For å beregne utveksling deler vi tanntallet til det drevne hjulet på tanntallet til det drivende. Tanntallet er antall tenner på tannhjulet.
Utvekslingsforholdet kan beregnes med formelen:
Et tannhjul med 10 tenner.
Merk at ved beregning med omdreiningshastighetene skal det drivende deles på det drevne, i motsetning til de to andre formlene der det drevne deles på det drivende. Dette er fordi tanntallet og diameteren er direkte omvendt proporsjonal med hastigheten. Mer tenner = lavere hastighet og vice versa.
Denne formelen gir også for eksempel at:
Z kan også erstattes med D o.s.v.
Disse formlene gjelder for alle typer tannhjul; sylindriske, heliske, koniske og snekkeskruer.
I eksempelet over går det drevne tannhjulet B 1 og 1/2 gang rundt for hver revolusjon av det drivende A. Vi kan skrive at utvekslingsforholdet er 1:1,5 men det ser ikke særlig pent ut. Vi bør heller skrive 2:3. Så hvor mange tenner har da A hvis B har f.eks. 20?
Først gjør vi om tanntallet til B og utvekslingsforholdet til brøk. Deretter deler vi tanntallet på forholdet ved å snu den bakerste brøken og gange som vanlig. Av det får vi et pent svar. Dersom vi får et desimalsvar er det noe som er feil. Vi kan ikke ha f.eks. 30,6 tenner på et tannhjul.
Sammensatte tannhjulssystemer
Med ett sett med tannhjul kan vi lage en hvilken som helst utveksling, men ved svært store utvekslinger blir enten det ene tannhjulet svært lite og vil ikke rotere ordentlig, eller det andre blir alt for stort til å være praktisk. Eller begge deler.
Derfor kan vi sette to tannhjul på den samme akselen og dermed lage et sammensatt tannhjulsystem (eng: compound gear train).
På illustrasjonen over er tannhjul B og C koblet sammen slik at de roterer med samme hastighet. Tannhjul A og B er i inngrep og tannhjul C og D er i inngrep. Dette skaper to utvekslingsforhold og systemets totale utveksling kalkuleres ved å multiplisere de to utvekslingene.
A = 36 tenner B = 18 tenner C = 32 tenner D = 16 tenner
Så hvordan regner vi andre veien? Si at vi har en utveksling på 24:1 som vi vil oppnå med så små tannhjul som mulig, men intet tannhjul skal være mindre enn 8 tenner. Vi kan gange begge sider med 8 å få 192/8 tenner som tilfredsstiller kravet til det lille tannhjulet men det drevne tannhjulet vil bli veldig stort.
24 kan faktoreres til 4x6 så vi kan lage en utveksling som gir 4:1 og en som gir 6:1. Ganger vi så dette med kravet om det minste tannhjulets tanntall, 8, får vi 32/8 tenner og 48/8 tenner som gir oss samme reduksjonen, men med totalt tanntall i systemet på 96 istedenfor 200 med mye mer kompakt konstruksjon. Dette kan gjøres enda mer kompakt ved å innføre enda et ledd i systemet som gir oss faktoren 2 x 3 x 4.
Mer informasjon i videoen under:
Snekkedrift
Reduksjoner med vanlige sylindriske tannhjul holdes normalt sett til ikke større enn 10:1. Dersom virkelig store utvekslinger kreves kan vi benytte snekkedrift som vanligvis benyttes mellom 10:1 og 500:1 reduksjoner.
Snekkedrift (eng: worm drive) eller skruehjulsdrift er drift der den tilførte kraften driver en skrue (eng: worm / worm gear) som er i inngrep med et tannhjul (eng: worm wheel) hvis aksel står 90 grader i forhold til drivskuren.
Snekkedrift brukes når svært stor utveksling kreves og er bygget på en måte slik at systemet selv-låser, det vil si at man kan bare tilføre kraft til skruen og når skruen ikke roterer vil hjulet ikke kunne rotere. Det er låst fast i gjengene på skruen.
Det finnes systemer der gjengene på snekkeskruen er vinklet slik at hjulet KAN drive skruen rundt, men dette medfører stor friksjon i systemet. Dette kalles omvendt snekkedrift.
På grunn av systemets selv-låsende natur egner det seg godt til f.eks. gitarer og andre strengeinstrumenter eller heisemekanismer.
Kalkulering av utveksling i skruehjulsystemer er nokså lik som normal utregning, men utvekslingen er antall tenner på snekkehjulet delt på antall gjengeinnganger på snekkeskruen (enkeltgjenget, dobbeltgjenget, trippelgjenget, o.s.v. ) Siden komponentene i systemet ikke opererer på samme måte kan vi ikke kalkulere utvekslingen ved delediameterne.
Dette er fordi én rotasjon av snekkeskruen forskyver snekkehjulet kun én tannfordeling, per gjengeinngang på snekkeskruen. En tregjenget skrue vil flytte hjulet 3 tanndelinger per rotasjon.
Skruehjulsystemer er designet slik at skruen og hjulet passer svært godt sammen, d.v.s. at tennene på snekkehjulet ofte er litt skråvendte får å passe gjengestigningen på skruen, samt at midten av tennene og tannbunnene er konkave for at skruen skal få så godt inngrep som mulig.
Koniske tannhjul
Dersom man ønsker å overføre kraft mellom to kryssende akslinger kan man benytte koniske tannhjul (eng: bevel gears).
Koniske tannhjul overfører kraft i en vinkel, og så lenge tuppen på de imaginære kjeglene møtes i samme toppunkt (eng: apex) kan man lage spisse, rette eller stumpe vinkler.
Tannhjulenes vinkel bestemmes av utvekslingsforholdet og tanntallet, og dersom en annen utveksling eller vinkel ønskes må begge tannhjulene byttes ut.
Den aller vanligste vinkelen er 90° og dersom tanntallet på de to tannhjulene er like kan dette på engelsk kalles "miter gears".
Det drivende hjulet i et tannhjulsystem kalles ofte "pinjong" (eng: pinion), spesielt i vinkeldrev der det drivende er mindre enn det drevne.
Vinkelen mellom akslingene er lik halvparten av de to kjeglevinklene.
Dette gir også at dersom man har en satt akselvinkel må summen av tannhjulenes konvinkel bli det dobbelte av akselvinkelen.
Heliske-, spiral-, og hypoid-tannhjul
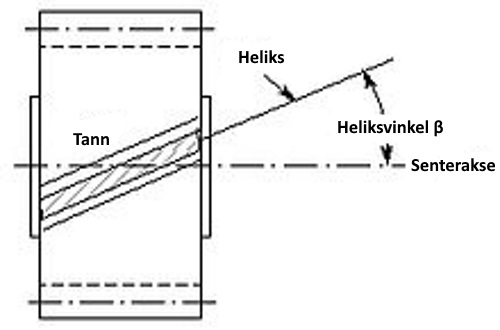
En heliks er en kurve langs en sylinder eller kjegle som roterer rundt et punkt og øker i høyde med en konstant vinkel.
Lengden av en rotasjon av heliksen er lik hypotenusen av omkretsen og høyden mellom to korresponderende punkter på sylinderen (pitch).
Heliske tannhjul er tannhjul der tannprofilen er kuttet skrått over dybden av tannhjulet. Dette gir økt total kontaktflate og bidrar til stillere og sterkere gang. Kalkulering av utveksling med heliske tannhjul fungerer som normalt.
To heliske tannhjul i inngrep må ha motsatt heliksvinkel (høyrehendt og venstrehendt)!
Siden tennene er vinklet skaper heliske tannhjul aksial motstand som bør tas hensyn til ved f.eks. å introdusere aksiale kulelagere.
Dette kan også motvirkes ved å lage dobbelt heliske tannhjul eller fiskebein tannhjul.
Spiraltannhjul er tannhjul der tennene er skåret ut fra en spiral med startpunkt i senter av tannhjulet. Disse gir enda mykere og stillere gang enn heliske tannhjul, men med mer friksjon. Det finnes flere forskjellige varianter av spiraler i bruk.
Spiralskårne tenner brukes som regel bare på koniske tannhjul.
"Zerol" tenner er tenner skårne etter en sirkel hvis senterpunkt er på tangenten til det koniske tannhjulets delesirkel med radius lik tannhjulets halve delesirkeldiameter og tangenten lik denne radius.
Kalkulering av utveksling med spiraltannhjul fungerer som normalt.
Hypoidtannhjul er koniske tannhjul der pinjongen ikke er på linje med kronhjulets senter.
"Hypo" er gresk og betyr 'under'.
Hypoidtannhjul kan oppnå enda større utvekslinger enn tradisjonelle koniske spiraltannhjul og kan betraktes som en hybrid mellom koniske tannhjul og snekkedrift.
Ved store nok spiraltenner vil systemet fungere svært likt som et snekkesystem ved at kronhjulet vil bli låst.
Hypoidtannhjul brukes mye i biler ved kraftoverføring mellom drivaksel og bakaksel.
Koniske spiraltannhjul som har kryssende senterlinjer er ikke hypoidtannhjul.
Modul og konstruksjon av tannhjul
I det metriske ISO system standardiseres kalkulering av tannhjul med en verdi som kalles 'modul'. Modulen til et tannhjul representerer størrelsen på tennene. Sammen med tannhjulets diameter og tanntall skaper det det hellige tannhjuls treenighet.
Modul er en enkel standard som definerer høyden, bredden og tykkelsen av tenner på et tannhjul basert på gitte parametere. Derav navnet "modul" av latin for 'enhet' eller 'forhold'. Den hellige tannhjuls treenighet sier at hvis du har 2 av 3 verdier kan du finne alt du trenger å vite om et tannhjul.
Det finnes også de vantro som ikke tror på den hellige Modul men heller vil bruke Diametral Pitch (hovedsaklig USA).
Modul og DP uttrykker det samme, men på motsatt måte, som man kan se i tabellen over.
Modul måler hvor hvor mange millimeter som går til hver tann.
Diametral pitch måler hvor mange tenner som går på en tomme.
Her ser man forholdet mellom Modul (over) og DP (under). Et høyere tall i Modulsystemet gir større tenner fordi det fordeler én tann over en større del av tannhjulet, men mindre tenner i DP-systemet siden det representerer flere tenner fordelt på den samme avstanden.
Begge systemer ender opp i 0,5 eller andre mindre-enn-én desimaltall, men på forskjellig ende av skalaen. 0,5 Modul betyr en veldig liten tann, mens 0,5 DP betyr en stor tann på to tommer.
For å konvertere mellom systemene kan følgende formler brukes:
Men for å virkelig forstå de hellige skrifter må vi først foreta en liten introduksjon til tannhjulets anatomi:
Det finnes mange rare og vanskapte tannhjul som ikke lar seg definere med modul, de går rundt, men disse vil ende opp i tannhjul-helvete når de kastes der alt er firkantet.
Delesirkelen er den interessante sirkelen her. Det er den vi kalkulerer alle de andre målene etter. Den går gjennom midten av tennene og representerer kontaktpunktet med det andre tannhjulet.
Tannhjul i inngrep møtes ved delesirkelen.
Tannhjul i inngrep må ha samme modul!
Senteravstanden mellom tannhjulene er summen av delesirkeldiameterne delt på to.
Så hvordan er dette magiske forholdet som modulen definerer?
Ved å bruke modul som en standard proporsjon kan vi kalkulere og produsere pålitelige tannhjul.
Hvis vi har en gitt utveksling som skal oppnås, d.v.s. vi vet tanntallet, og vi vet modulen kan vi kalkulere hvor stort tannhjulet blir og deretter alle de andre målene vi trenger.
Hvis vi har en gitt størrelse og tanntall kan vi finne ut hva modulen må være for å få et korrekt og velfungerende tannhjul.
Hvis vi vet modulen og størrelsen kan vi kalkulere tanntallet.
Delingen er avstanden mellom tennene målt fra to like punkter på hver tann på delesirkelen som den får sitt navn fra.
Delingen kalkuleres slik:
I land som bruker diametrisk deling (Diametral Pitch (DP)) bruker de også tommer og Circular Pitch (CP) finnes ved å erstatte Modul med DP i formelen over.
Her står m for modul, ikke meter...
Andre kjekke formler:
Toppsirkeldiameteren da = (Z+2)m fordi da = z*m + 2*m siden den er èn ganger modulen lenger ut på begge sider, derav +2 o.s.v.
Etc... Flere andre formler kan ekstrapoleres via det som er gitt, over er bare noen eksempler.
Ved kalkulering av sylindriske tannhjul med heliske tenner er det to måter å produsere de på. Enten ved å bruke 'Pn' som er "pitch normal" eller 'Pt' som er "pitch transverse". Pt er den transverse delingen, det vil si sett radialt på hjulet (ovenfra). Pn er den normale delingen sett fra siden. Siden tennene er skrå er den transverse modulen Mt lenger enn den normale Mn som gjør at man må endre verktøyet etter heliksvinkelen dersom man skjærer tannhjul med det transverse system, men med det normale system kan man bruke det samme verktøyet uavhengig av heliksvinkelen.
Ved kalkulering av koniske tannhjul er det vinklene som definerer tennene, ikke diameteren.
Det finnes også koniske tannhjul med ikke-vinklede tenner. I disse tilfellene brukes diameterne istedenfor vinklene for kalkulering.
Når det kommer til snekkesystemer er det tre forhold å ta hensyn til, aksial modul, normal modul og transvers modul.
Her sett fra den aksiale vinkel.
Px er den aksiale delingen, Pn den normale og Pt den transverse.
β er stigningsvinkelen og er den samme som snekkehjulets heliksvinkel.
Pressvinkelen er en faktor som bidrar til å bestemme tannprofilen. Før var det vanlig med en pressvinkel på 14,5 grader, men i dag er det mer vanlig med 20 grader spesielt i evolventfortanning. Evolventfortanning er tenner med en profil som sørger for konstant kontakt mellom tannhjulene og jevn overføring av kraft.
Tannhjul har fasetterte tenner for at tennene skal gå klar av hverandre. Hadde tennene vært helt firkantet ville de låst seg.
Evolventen av en sirkel er kurven som dannes når man vikler en imaginær tråd stramt av sirkelen.
Det er altså en del av omkretsen dratt ut fra et punkt på sirkelen til tangenten til punktet med samme lengde som stykket med omkrets som er viklet av.
Det viser seg at evolvente kurver er ypperlig til bruk i tannhjul. De gir en konstant kontakt og jevn pressvinkel.