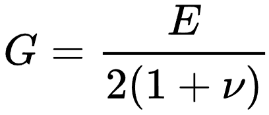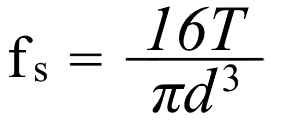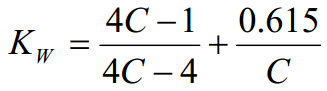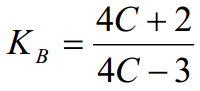Spring Theory
/Fjærer er et meget utbredt og viktig mekanisk element som bidrar til at nesten alt vi bruker til daglig skal fungere. Det er vanskelig å peke på noe mekanisk som ikke inneholder en eller flere fjærer av et eller annet slag.
Fjærer finnes i et uendelig utvalg utførelser og er ofte spesialdesignet til formålet. Man får kjøpt sett med standard størrelser og krefter, men ofte i dyrere og mer avanserte innretninger må fjærer beregnes, designes og produseres etter unike spesifikasjoner.
En fjær er en mekanisk innretning som lagrer mekaniske krefter i form av potensiell energi. De er som oftest laget av fjærstål, som er et høy-kvalitets stål med et høyere karboninnhold (mellom 0,4% - 1,05%) enn vanlig maskinstål (mellom 0,05% - 0,3%) , samt høyere verdier av andre varierende grunnstoffer som mangan, svovel, fosfor, silikon, krom og nikkel. Fjærer kan også være laget av andre ting som plast, gummi, tre eller lignende. En bue er for eksempel i bunn og grunn en stor bladfjær av tre.
Typer fjærer
Fjærer kommer som sagt i mange utførelser og varianter, men de vanligste former og bruksområder er som følger:
Kompresjonsfjær
Kompresjonsfjærer er kanskje den vanligste typen mekanisk fjær og er antakeligvis den formen man tenker på når man tenker på en fjær. De er ofte laget av ståltråd som er viklet i en heliks med godt mellomrom mellom viklingene og flate ender. Disse lagrer energi når de blir komprimert i den aksiale rettningen. Brukes i alt mellom himmel og jord der noe må dyttes eller holdes fra hverandre eller på plass, men fortsatt kunne bevege seg.
Ekspansjonsfjær / Trekkfjær
Ekspansjonsfjærer er også ekstremt vanlige og fungerer på samme måte som komresjonsfjærer, bare motsatt. De er ofte laget på samme måte som kompresjonsfjærer, men viklingene ligger tett inntil hverandre og endene har ofte kroker til å hekte i det som skal trekkes sammen. Disse lagrer energi når de blir trukket fra hverandre og avstanden mellom viklingene øker. Brukes også overalt, men ofte i dører og andre ting som skal være trukket sammen i normal tilstand.
Torsjonsfjær
Torsjonsfjærer er enda en veldig vanlig type fjær, men den fungerer på en annen måte enn de to overstående typene. I stedet for å lagre energi ved å endre lengde aksialt, bygges energien opp ved å bøye viklingene radialt, eller vinkelrett fra aksen, rundt aksen. De er laget mye på samme måte som ekspansjonsfjærer, men hakene er strukket rett ut tangentielt fra fjæren. Brukes ofte på samme måte som kompresjonsfjærer, men der det ikke er plass til å ha en slik vinkelrett på flaten som skal dyttes. Brukes f.eks. i klesklyper.
Spiralfjær
Spiralfjærer er, som navnet tilsier, viklet i en spiral og lagrer energien ved å slange seg rundt seg selv og vil bli mindre i diameter. En spiralfjær har ganske lang arbeidslengde siden den strammes rundt seg selv og kan trekkes flere ganger rundt. De har ofte et fast punkt i midten hvor de er festet til et statisk punkt i maskinen og den yttre haken driver noe rundt i sirkel. Brukes mye i urverk.
Volutt fjær
Volutte fjærer er på en måte en blanding av spiralfjærer og kompresjonsfjærer i det at viklingene overlapper hverandre i en spiral mens det dannes en konisk heliks av båndet. Disse fjærene har høy belastningsevne og er selvrettende, d.v.s. de bøyer seg ikke like mye ut til sidene dersom de blir belastet uten ekstern støtte som f.eks. ekspansjonsfjærer av viklet tråd. De kan derfor brukes alene uten støtte. Disse ser man brukt på tenger og annet verktøy.
Belleville-fjær
Belleville-fjærer er flere belleville-skiver stablet oppå hverandre til å skape en økt fjærende funksjon og øke arbeidslengden. En belleville-skive er en skive som er bøyd til en konisk form og brukes som låseskiver på bolter for å skape økt motpress på bolten. Flere av disse vil som sagt danne en belleville-fjær. De har begrenset arbeidslengde, men tåler høy last.
De kan stables i serie eller parallel. I serie stables de motsatt om hverandre slike at tuppene møtes innerst og ytterst om hverandre. I parallel legges de samme vei flere av gangen. Serie vil øke arbeidslengden, mens parallel vil øke kraften som trengs for å komprimere den.
Det er en veldig modulær form for fjær, men trenger støtte enten i midten eller på utsiden for å fungere.
Bølgefjær
Bølgefjærer er en form for kompresjonsfjærer med noen fordeler. De er kveilet med flatt stålbånd som blir bølget, og det er disse bølgene som skaper den fjærende effekten. Evnene til en bølgefjær kan endres ved å endre tykkelsen og bredden på båndet, antall bølger, høyden på bølgene og antall viklinger. Blandt fordelene denne gir er at arbeidslengden kan mer eller mindre halveres mens kraften forblir den samme sammenlignet med tradisjonelle tråd-fjærer.
Bladfjær
Når vi sier bladfjær tenker nok mange på de store fjæringssystemene på biler og vogner og slikt, men som børsemakerelev har ordet en litt annen betydning for meg.
En bladfjær er i bunn og grunn den enkleste formen for fjær; en flat bit med rett, vinklet eller bøyd stål. En bladfjær har vanligvis ikke gjentagende former (med mindre det er en trekkspillfjær) i motsetning til alle andre tidligere nevnte fjærtyper. Brukes overalt, du har helt sikkert en av plastik på kulepennen din.
<-- Magasinfjær (trekkspillfjær, som er en form for bladfjær)
Det finnes mange andre typer og former av fjærer, mange flere enn jeg kan ramse opp, men andre fjærer som kan være vanlig å støte på er stort sett varianter av kompresjonsfjærer og andre heliks-fjærer som dette:
Ikke-lineære fjærer er interessante fordi ved å endre avstanden mellom viklingene kan man endre hvordan fjæren oppfører seg og dermed oppnå en fjæring som ikke er konstant over hele fjærens arbeidslengde. Alle fjærene i bildet over er teknisk sett ikke-lineære, dog begrepet brukes hovedsaklig om fjærer med konstant diameter, men ulik viklingsavstand:
Det finnes også nestede fjærer, som er en fjær med en fjær inni seg. Disse er viklet motsatt vei for å hindre at de to fjærene hekter seg opp i hverandre. Disse brukes hvis én fjær ikke er nok og det ikke er plass til en større fjær, eller som backup hvis hovedfjæren skulle ryke. De kan også drive forskjellige ting på samme akse.
Fjærens anatomi
Parametriske verdier:
D = Fjærens effektive diameter, kan finnes ved å bruke formlene til høyre -->
d = Trådens diameter
Di = Interne diameter
De = Eksterne diameter
L0 = Total lengde
Lr = Arbeidslengde, den lengden fjæren "fjærer" på
Lc eller Ls = Solid lengde, fjæren kan ikke komprimeres forbi dette punktet (med unntak)
P = Viklingsavtand (pitch)
α = Heliksvinkel, målt i fjærens frilengde, vil endre seg ettersom fjæren blir komprimert.
nt = Totalt antall viklinger
n eller na = Aktive viklinger
ne = Endeviklinger
Endeutførelse er måten endene på fjæren er bearbeidet på og vil påvirke hvordan aktive viklinger telles:
Måter å finne fjærens diameter på.
Det er viktig å påpeke at én vikling av en fjær med de samme karakteristikken som en lenger fjær tåler akkurat like mye last, det eneste vi oppnår med flere viklinger er å spre lasten ut over en lengre distanse slik at vi får en lengre arbeidslengde.
Fjærindeks C
D og d brukes igjen til å regne ut C som representerer fjærindeksen:
f.eks. vil en fjær med effektiv diameter 12mm og en trådtykkelse på 1,5mm ha en indeks på 8. En fjær på 16mm med 2mm tykk tråd vil ha samme indeks. Indeksen representerer formen og egenskapene til fjæren. De fleste kompresjonsfjærer har en indeks fra 6 til 12.
Fjærer med indeks 4 eller under er små med tykk tråd og er vanskelig å produsere fordi tråden må bøyes veldig kraftig og kreftene på verktøyet er store. En indeks på 1 vil si at fjærens interne diameter er lik 0.
Fjærer med indeks 25 eller mer er store med tynn tråd og er også komplisert å produsere til eksakte mål. De er vanskelig å ha med å gjøre siden de oppfører seg som trappetroll og har generelt sett ingen praktisk verdi. Veldig store verdier for C vil ende opp med at fjæren kollapser under sin egen vekt på grunn av den forholdsvis tynne tråden.
Fjærindeksen brukes for å regne ut en del andre verdier for en gitt fjær.
Hookes Lov
Hookes Lov, oppkalt etter 1600-talls fysiker Robert Hooke, sier at kraften en konvensjonell fjær utøver er proporsjonal med endringen i lengde og uttrykkes slik:
Der F er den kraften i Newton som dytter mot det som komprimerer fjæren, hvilket også er årsaken til minustegnet foran k som representerer at det er den gjenopprettende kraften til fjæren, den beskriver altså bare retningen til kraften. X er endringen i lengde i meter, altså distansen fjæren har beveget seg fra den opprinnelige frilengden. k er et forhold (eng: spring rate / spring constant) som avhenger av fjæren; trådtykkelse, viklingsavstand, diameter, materialtype, etc. k kan finnes ved å fysisk måle avstanden en fjær beveger seg når den blir utsatt for en kraft. k = F/X som oppgis i N/m eller Newton per meter (ikke Newtonmeter (Nm)). Dette forholdet kan også oppgis som R for 'rate'. Hookes lov beskriver en ideell fjær, men er en god tilnærming til de fleste ekte fjærer. En annen måte å si det på er at; motpresset i et objekt er lik den påførte belastningen innenfor det elastiske området til objektet.
Hvis vi vet dette forholdet k kan vi regne ut hvor mye kraft fjæren utøver ettersom hvor sammenklemt eller utstrukket den er. Dette fordrer selvsagt at all denne endringen i lengde foregår innenfor fjærens elastiske grenser:
Den midterste fjæren i bildet til høyre representerer fjæren i avslappet tilstand. X-aksen viser endring i lengde mens Y-aksen viser påført belastning.
Ettersom den blir komprimert vil X synke proporsjonalt med belastningen helt til fjæren når sin solide form og vil ikke kunne komprimeres ytterligere; som vises på grafen der belastningen øker, men komprimeringen avtar.
Når fjæren trekkes ut gjelder også Hookes lov som er representert av den røde linjen. Den stiplede grå streken viser hvordan fjæren oppfører seg i virkeligheten. Vi kan se at etterhvert som vi drar fjæren ut over dens elastiske grense vil den begynne å deformere seg helt til den er trukket helt rett ut og vi vil se den samme økningen i belastning mens endringen i lengde avtar opp til det punktet at tråden ryker.
Torsjonsfjærer følger en angulær form for Hookes lov:
Der:
τ (tau) = Det påførte momentet i Newtonmeter
k = Fjæringskonstanten
θ (theta) = Vridningen av fjæren fra hvileposisjonen i radianer, mer om radianer her
Elastisk og plastisk deformasjon og Youngs modulus
Plastisk og elastisk deformasjon er viktige begreper innen fjæring, men gjelder så godt som alle materialer. Belastning (stress) og påkjenning (strain) [eller motpress eller deformering] er verdier som brukes for å beskrive defleksjon, eller hvor mye et materiale er tilbøyelig til å endre seg dimensjonalt under så og så mye påført kraft, og kurven som brukes for å beskrive disse verdiene definerer også ofte punktet der materialet vil bli påført permanente endringer og når det brekker.
Elastisk deformasjon er når materialet blir påført kraft slik at det bøyer seg og deretter returnerer til sin opprinnelige form når belastningen blir fjernet.
Plastisk deformasjon forekommer når materialet blir bøyd over dette punktet og all bøying etter dette blir permanent endring når belastningen opphører.
Belastningen kan måles og oppgis i Pascal (trykk) eller Newton per kvadratmeter, som er definisjonen på en Pascal, mens påkjenningen (som er et fellesbegrep som varierer fra materiale til materiale og er også et forhold og er dermed dimensjonsløst) måles i graden av endring i materialet i kraftretningen og oppgis vanligvis i meter per meter; men: det er mer korrekt å si at det oppgis i lengde per lengde, siden påkjenningen som sagt er et forhold mellom endringen i lengden på materialet og materialets opprinnelige lengde, og ettersom materialet blir utsatt for økende trykk så vil dette forholdet øke. Vi må bruke et forhold siden selv om egenskapene til materialet vil være likt i ulike tilfeller så vil materialets faktiske mengde / fysiske størrelse påvirke hvordan det oppfører seg. Det er lettere å bøye noe tynt enn noe tykt, men i forhold til tykkelsen vil materialet oppføre seg likt.
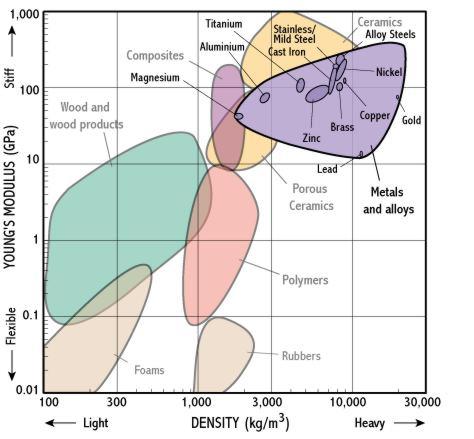
Det er her Young's modulus kommer inn i bildet. Oppkalt etter 1800-talls vitenskapsmannen Thomas Young (men konseptet ble oppfunnet av den legendariske Leonhard Euler) og definerer stivheten til materialer. Youngs modulus kalkuleres ved å ta belastningen delt på påkjenningen, som gir enda et forhold: Y. Kan også være E for 'elastic modulus'. Youngs modulus oppgis vanligvis i megaPascal eller gigaPascal, men er også i grunnen dimensjonsløst.
En lav verdi, f.eks. 0,1 vil si at materialet er veldig fleksibelt og mykt siden 1 enhet belastning tilsvarer 10 enheter påkjenning. Dette vil si f.eks. gummi.
En høy verdi, f.eks. 100 tilsier at materialet krever et trykk på eksempelvis 200 enheter belastning for å endre seg 2 enheter lengde. Som f.eks. glass
Altså brukes Youngs modulus til å forutsi dimensjonale endringer i materialer under strekk eller press. Det er også viktig å påpeke at Youngs modulus er en lineær funksjon og er brukbar kun innenfor det elastiske området til materialet, altså kan den bare brukes der Hookes lov gjelder.
Poissons forhold
Poissons forhold er et forhold som beskriver den tverrgående endringen i tykkelse i et materiale når det blir utsatt for en langsgående påkjenning. Det er strengt tatt ikke nødvendig å bruke ved produksjon av alminnelige fjærer, men det er kjekt å vite om.
Når en stang blir strukket ut må det materialet som gjør at stangen blir lengre komme fra et sted, og det blir da tatt fra tykkelsen. Og motsatt; dersom stangen komprimeres vil diameteren øke.
ε long står for 'longitudinal' og er endringen i lengderetningen. kan også hete ε axial.
ε lat står for 'latitudinal' og er endringen i diameter. Kan også hete ε trans.
Forholdet uttrykker altså forholdet til endringen i bredde delt på forholdet til endringen i lengde. Minustegnet er der for at forholdet skal ha en positiv verdi ettersom svaret vil bli et negativt tall. Forholdet betegnes med den greske bokstaven 'nu': ν. Blir noen ganger skrevet med 'my'; µ.
De fleste materialer har en verdi mellom 0 og 0,5. Her er en tabell over vanlige materialer og deres Poisson-tall:
Som man kan se av tabellen så har kork en verdi på rundt 0, det vil si at den så godt som ikke opplever tverrgående ekspansjon under aksial kompresjon eller tverrgående sammentrekning under aksialt strekk. Mens gummi har en verdi nærme 0,5 som vil si at den opplever stor endring i tykkelse når det blir sammenpresset eller trukket fra hverandre.
Så hvis vi trenger å vite hvor mye en tråd krymper i diameter når den blir strukket kan vi bruke en variasjon av formelen slik:
Formelen over er kun gyldig for små størrelser, dersom større utslag skal kalkuleres bør man benytte denne formelen:
Poissons forhold er mer komplisert enn dette, spesielt i ikke-sirkulære objekter og det finnes også materialer som ikke følger denne regelen og utvider seg når de blir strukket, men for en grunnleggende forståelse og bruk er formlene over nok.
Bruddstyrke og belastningstyper
At vi kan beregne hvor mye et materiale vil bøye eller strekke seg er vel og bra, men det viktigste ved design av fjærer er vel egentlig hvor mye last de tåler før de brekker. Hvis vi kan designe en fjær som leverer det motpresset eller energien vi trenger og vite at den ikke kommer til å brekke under normale belastninger så er jobben vår gjort.
Noen fjærer er ikke designet for å bevege seg i hele arbeidsområdet sitt. Bilfjærer for eksempel har ikke godt av å bli komprimert helt ned til sin solide posisjon. De tåler det sikkert, men de er ikke 'laget' for det.
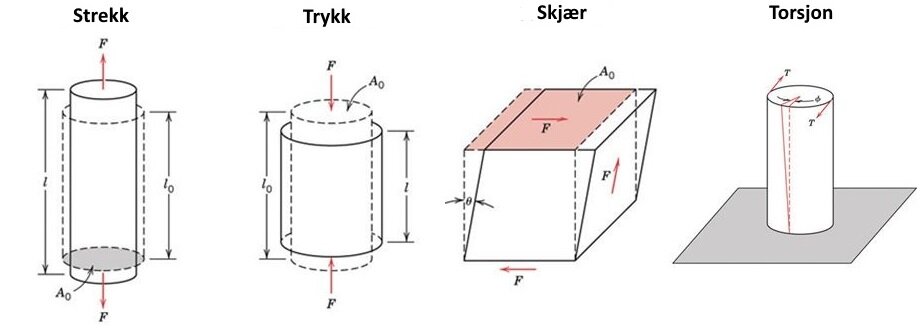
Det er hovedsakelig tre former for belastning; strekk, trykk og skjær.
Strekk- og trykkbelastning er krefter der påkjenningen og det eventuelle bruddet forekommer vinkelrett på kraftretningen, mens ved skjærende belastning blir påkjenningen parallell med kraftretningen.
På engelsk heter dette henholdsvis 'tensile stress', 'compressive stress' og 'shear stress'.
Her er en vikling av en fjær. Fjæren i sin helhet blir selvsagt utsatt for strekk- eller trykkbelastning, men inne i fjæren er det noe annet som fører til den fjærende effekten.
Når A og B trekkes fra hverandre eller dyttes mot hverandre vil det forårsake vridning i punkt C. Vridning i et materiale, eller torsjonal belastning er en form for skjærbelastning.
Generell skjærbelastning er en funksjon av kraften over arealet av tverrsnittet:
Generell skjærbelastnig betegnes med den greske bokstaven 'tau' τ.
Ren skjærbelastning i f.eks. en stang som vris kan finnes ved:
γ (gamma) = Påkjenningen
G = Belastningsmodulusen til materialet (shear modulus / torsional modulus of elasticity)
γ kan vi finne slik:
ρ (rho) = En avstand fra senter av sylinderen i meter, vanligvis c
φ (phi) = Vinkelen på vridning i radianer, betegnes også noen ganger med θ (theta)
L = Lengden på det vridde elementet i meter
c = Radien til sylinderen i meter
T = Det påførte momentet i Newtonmeter (Nm)
Torsjonspåkjenningen er altså et resultat av vridningen over en avstand av materialet. Påkjenningen øker proporsjonalt med avstanden fra senter, det er minst påkjenning i midten av sylinderen og mest ved omkretsen der endringen er størst. Dersom man vil finne påkjenningen et sted langs radien endrer man ρ til noe annet enn c, som foreksempel c/2 som finner påkjenningen halvveis mellom senter og omkretsen.
Skjærbelastnings-modulusen G finner vi av følgende formel:
Her ser vi at modulusen avhenger av både Youngs modulus og Poissons forhold. Det er også resultatet av den skjærbelastningen delt på den torsjonale påkjenningen.
Praktiske formler
For å regne ut diverse egenskaper til fjærer med de fysiske data vi har tilgjengelig finnes noen praktiske formler:
Fjæringskonstanten k kan finnes fra denne formelen:
Maksimal torsjonal belastning for en fjær gis ved:
fs = Maksimal belastning (max shear force)
T = Momentet (torque) i Newtonmeter. Momentet er som kjent kraft ganger arm, og i dette tilfellet er kraften den påførte lasten på fjæren i Newton og armen er D/2 siden armen regnes fra senter av fjæren og påvirker begge sider av viklingen likt. Så dette gir:
Der W er belastnigen i Newton. Så for å finne maksimal last for en gitt tråd før den ryker kan vi snu formelen:
Men det fordrer at vi vet hvor mye torsjonal belastning tråden tåler.
Som vi kan se av disse formlene er lasten en fjær tåler proporsjonal med tykkelsen på tråden og omvendt proporsjonal med diameteren på fjæren. Ved å doble trådtykkelsen blir fjæren 8 ganger så sterk og ved å doble fjærdiameteren blir fjæren halvparten så sterk.
Hvor stor endringen i lengden på fjæren vil være uten å vite fjæringskonstanten kan regnes ut slik:
Kurve-effekten og Wahl-faktor
Mange av disse og følgende kalkuleringer går utifra at tråden i fjæren er rett, men det er den jo ikke. Tråden i viklingene bøyer seg naturligvis og dette medfører ekstra former for belastning på tråden τ og fjæringsforholdet k. Materialet i tråden vil strekke seg på utsiden av fjæren og komprimeres på innsiden av fjæren. Dette kalles kurve-effekten og Wahl-faktoren er en verdi K vi modulerer med for å korrigere for denne effekten.
I grafen over er K1 Wahl-faktoren som modulerer belastningsgrensen. Formelen for denne faktoren bruker fjærindeksen C og ser slik ut:
Denne verdien ganges da med resultatet fra belastningsberegningen slik at vi får:
Det finnes en lignende formel som beregner det samme og er kjent som Bergsträsser-faktoren:
Forskjellen mellom Wahl og Bergsträsser er mindre enn 1% så Bergsträsser er å foretrekke.
K2 korrigerer fjæringskonstanten k:
Slik at vi får:
I praksis
Jeg ble interessert i design av fjærer og satte meg inn i det da jeg lagde et viklingsverktøy til dreiebenken. Den mater en tråd opp til 2mm tykk presist rundt en stang som står i kjoksen og ved bruk av maskinmating kan jeg kontrollere viklingsavstanden.
En bit med stål med et spor i kan presses mot tråden for å øke friksjonen og holde igjen tråden slik at den strammer seg og legger seg godt rundt stangen. Tråden jeg bruker kalles 'pianotråd' eller 'music wire' å kommer ferdig arbeidsherdet fra fabrikken og kan vikles i kald tilstand.
Siden den allerede er herdet og anløpt har den en høy Youngs modulus og vil 'sprette' tilbake til en større fjærdiameter enn det den blir viklet til, så stangen man bruker må være mindre enn den interne fjærdiameteren man ønsker. Det finnes tabeller for dette.
En fjær må ikke lages slik at viklingsavstanden overstiger den plastiske deformasjons-grensen til tråden, ellers vil den aldri tilbakestille seg til opprinnelig lengde etter full kompresjon. Dette kan derimot noen ganger være av design ettersom materialet vil "sette seg".
For andre materialer som ikke er herdet må vi herde fjærene etter at er viklet, disse er også lettere å vikle.
Når vi herder låser vi fast stålet i en konfigurasjon med veldig liten elastisk rekkevidde og kort plastisk deformasjon før det når bruddpunktet, ved å anløpe det avslapper vi stålet nok til å utvide det elastiske området drastisk.