Hydraulikk og pneumatikk

/

Hydraulikk og pneumatikk er svært effektive og smarte måter å overføre mekanisk kraft på. Væsker og gasser har den egenskap at de former seg til omgivelsene og sprer seg likt utover hele det området de har tilgjengelig. De er "smidige" og kan overføre kraft på rare måter og i merkverdige vinkler.

Ordet hydraulikk kommer fra latin, 'hydro' som betyr "vann" og pneumatikk kommer av ordet 'pneuma' som betyr "pust" eller "sjel".

Hydraulikk er læren om væske i bevegelse og trykk i mekaniske systemer, rettere kalt hydrodynamikk og hydrostatikk respektivt.

En fundamental egenskap med væsker er at de er så godt som ukomprimerbare. Det vil si at de er veldig egnet til å omdirigere trykk og kraft.

Dette er hovedforskjellen mellom hydraulikk og trykkluft, siden trykkluft baserer seg på gass, hvilket ER komprimerbar. Væske er teknisk sett komprimerbar, men det komprimerer seg maksimalt ca. 1,5% under enormt trykk.

Hydraulikk brukes når man trenger ren kraftoverføring. Trykkluft brukes i systemer som trenger å slå raskt ut eller være fjæret, som luftfjæring i biler.

Siden ca. 1950 har hydraulikk vært standard teknologi i konstruksjonsmaskiner og er i dag brukt overalt i tung industri, styresystemer, bremsemekanismer, etc. og spiller en stor rolle innen gruvedrift, landbruk m.m.

Pneumatikk er på mange måter likt som damp med tanke på at begge bygger på å komprimere gass, men hovedforskjellen er hvordan de oppnår trykket. Dampdrift oppnås ved å koke vann og lage vanndamp under høyt trykk, noe som skaper veldig mye energi og er hvordan de fleste atomreaktorer lager strøm. Men dampen blir til vann igjen når den avkjøles og den er varm når den er i bruk. Trykkluft er også komprimert gass, men den komprimeres med en kompressor og er kald når den kommer ut og kondenserer ikke slik at den kan brukes på mange felt der damp ville vært upraktisk.

Trykkluft er ikke like effektivt som hydraulikk når det kommer til tungt maskineri, men har mange andre bruksområder og er en svært utbredt teknologi som brukes i transport, styresystemer, fjæringssystemer, robotikk, målesystemer og mye annet. Pneumatikk er også på mange områder "raskere" enn hydraulikk pga. lavere viskositet, mer om det senere.

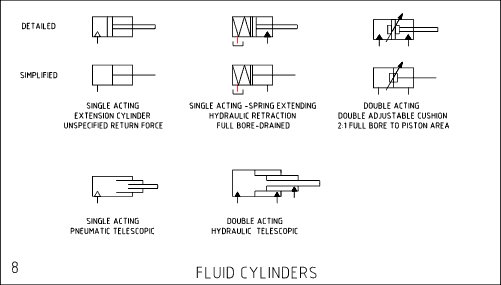
Pneumatiske sylindre (Pneumatic actuators)

Pneumatiske sylindre (Pneumatic actuators)

Hydrauliske sylindre (Hydraulic actuators)

Hydrauliske sylindre (Hydraulic actuators)

 

Fundamentale prinsipper innen hydraulikk

Grunnprinsippene innen hydraulikk er ofte kreditert til den franske fysikeren Blaise Pascal, og som så mange vitenskapsmenn fra den tiden har han selvsagt en lov og enhet oppkalt etter seg.

Pascal's lov sier at en trykkendring som forekommer hvor som helst i et lukket system med ukomprimerbar væske sprer seg slik at det samme trykket er likt overalt i systemet.

Grunnprinsippene er:

  1. Væsker former seg til beholderen

  2. Væsker er praktisk sett ukomprimerbare

  3. Væsker sprer trykk likt i alle retninger

 

Væsker former seg til beholderen

Væske vil spre seg likt ut til samme nivå og ut i alle kriker og kroker som væskens trykk overkommer.

 

Væsker er praktisk sett ukomprimerbare

Væsker komprimerer seg ca 1-1,5% under et trykk på 20000 kPa (kiloPascal). Hydraulisk olje, hvilket er det som stort sett blir brukt i slike systemer regnes for å være så godt som ukomprimerbar, samt at den smører systemet og hindrer korrosjon.

Væskens molekyler ligger pakket slik at de ikke lar seg pakke tettere. Økt trykk på systemet øker trykket, men væskens volum forblir det samme.

 

Væsker sprer trykk likt i alle retninger

Trykket i et hydraulisk system er likt overalt i systemet.

I flasken til høyre, som er et ofte brukt eksempel på Pascals lov, påføres det et trykk på korken. Dette trykket er likt i hele flasken pga. væsken.

Når en sylinder er koblet til en annen lik sylinder via en slange eller rør vil en volumendring i den ene sylinderen gi en lik volumendring i den andre sylinderen. Trykket i systemet vil være likt overalt.

Væsker er praktiske for å overføre kraft gjennom slanger og rør, gjennom hjørner og andre rare vinkler og veier.

Trykk-trekanten

Trykk i hydrauliske og pneumatiske systemer måles i Pascal.

  • 1 Pascal er 1 Newton per kvadratmeter

  • 1 Newton er kraften som trengs for å gi 1 kilo en hastighet på 1m/s på ett sekund

  • 1 Kilogram er lik 9.80665002864 Newton, som er tyngdekraften til jorden. Dette blir vanligvis rundet av til 9,8 Newton, eller 10 om man er grov i målet .

  • Trykk benevnes som oftest i kiloPascal (kPa)

  • Trykk beskrives også i Bar. 1 Bar er lik 1 atmosfære (atm) (nesten; det er 1.01325 Bar) og er trykket ved havnivået

  • 1 kPa er 1/100 Bar, altså er 1 Bar = 100 kPa eller 100 000 Pascal (10⁵ ). 1 MegaPascal (MPa), 1 million Pascal = 10 Bar

Formlene er som følger:

  • Kraft = Trykk x Areal (F = p x A)

  • Trykk = Kraft / Areal     (p = F / A)

  • Areal = Kraft / Trykk     (A = F / p)

Det er litt forvirrende når vi er vant til metrisk at alle enheter er delelige på 1000 med hverandre or er direkte relaterte at 1 Bar er 100 000 Pa, men det får vi leve med.

I det imperiske system brukes PSI for å måle trykk som står for "pound-force per square inch" og jeg må ærlig talt innrømme at jeg er litt misunnelig på akkurat denne måten å benevne det på. Ja, Pascal gjør akkurat den samme jobben, mye bedre også siden den er en SI enhet, men med PSI er hele formelen oppgitt i enheten og enheten er kun et amalgam av de to variablene man behøver for å finne den;

  • Kraft måles i pund hvor ett pund er 4.44822 Newton

  • Areal måles i kvadrattommer hvor en tomme er 2,54 cm og en kvadrattomme er 0.00064516 m²

 

Atmosfærisk trykk og vekten av vann

I tillegg til trykket man tilfører hydrauliske og pneumatiske systemer er det som sagt et konstant trykk på alt som befinner seg på bakkenivå, kalt 1 atmosfære trykk. Luft veier ikke stort, men når man regner med all luften som befinner seg innen en søyle på 1 kvadratmeter fra bakken og opp til kanten av atmosfæren blir vekten betydelig, ca 10 tonn! Dette trykket som befinner seg på bakkenivå, og som vi alle opplever, kalles en standard atmosfære og er som sagt lik 101 325 Pa, ofte avrundet til 100 000 Pa, som er 1 Bar eller 14,7 PSI.

De fleste trykkmålere kompenserer for dette trykket og viser 0 kPa ved bakkenivå, altså standardtrykk. Trykket i et system som også tar hensyn til atmosfærisk trykk refereres til som absolutt trykk. Når trykket ved havnivået går under atmosfærisk trykk i et system kalles dette et vakuum, og absolutt vakuum vil tilsvare et absolutt trykk på 0 kPa.

Når man dykker er trykket på den dybden man dykker til ofte oppgitt i atmosfærer.

En kubikkmeter vann inneholder 1000 liter og veier da 1000 kg. 1 kubikkmeter vann utgjør en kraft nedover på 9806.650 Newton så med litt matte kan vi regne oss frem til at 1 atmosfæres trykk under vann oppstår 101 325 / 9806.650 = 10, 3 meter under vann. Så når vi befinner oss 10,3 meter under vann opplever vi 2 atmosfærer, vekten av luften pluss vekten av vannet over oss. 20,6 meter ned er da 3 atmosfærer, osv...

 

Så hvordan funker det i praksis?

Den fundamentale tredje egenskapen til hydraulikk og pneumatikk, at trykket sprer seg likt i alle retninger vil da si dersom man påfører et trykk i en væske vil trykket påføre størst kraft på den største overflaten. Trykket er likt overalt, men siden kraft = trykk X areal vil et større areal ha større kraftpotensiale.

Tegningen over et typisk eksempel for å forstå konseptet. En kraft F1, la oss si 50 N, trykker på stempel A1 som har en overflate eksponert til den hydrauliske væsken på 0,001 m², hvor stort trykk blir det i væsken?

Så hvis stempel A2 har et areal på 0,01 m², hva blir da kraften vi får ut i F2?

Vi ser at med en 10-dobling av arealet har vi 10-doblet kraften vi puttet inn i systemet. Dette er på mange måter det samme forholdet som gjelder for tannhjul. Et tannhjul som drives av et 10 ganger mindre tannhjul vil ha 10 ganger kraften som blir tilført det drivende hjulet, men det lille hjulet må gå 10 ganger rundt for at det store skal gå en gang rundt. Det samme gjelder hydrauliske systemer. Hvis man 10-dobler arealet får man 10 ganger kraften, men stempelet går bare 1/10 av distansen som det lille gjør. Så man må presse det lille stempelet 10 ganger så langt som den distansen man vil oppnå med det store.

Det motsatte er også sant som man kan observere på f.eks. sprøyter. Det krever en del trykk for å presse ut væsken, men den skyter ut fortere og mye lengre ut av kanylen enn det man presser på sprøyten.

En liten kraft over en lang avstand erstattes med en stor kraft over en liten avstand og vice versa.

Siden trykket i systemet er likt overalt vil et trykk på 1 Pa være 1 Newton per kvadratmeter, så når man får dette trykket til å trykke på noe som er 10 kvadratmeter vil trykket på den flaten være 10 Pa! Magi!

Så dersom jeg vil løfte en hel bil med en hydraulisk jekk, kun med min egen kroppsvekt, hvor bilen veier 1,5 tonn og jeg veier 65 kilo, hvor liten må sylinderen jeg står på være?

Vel, min kroppsvekt har en kraft på 637.432 Newton mot bilens 14709.975 N. Vi kan med en gang se at sylinderen må være (14709 / 637 = 23,1) hvertfall over 23,5 ganger mindre enn drivstempelet, som er 0,05 m², som gjør at den må bli 0,0022 m² eller mindre.

Stemmer det?

Med bare bilen på jekken påfører den et trykk på systemet på p = 14709.975 / 0,05 = 294,2 kPa. For at jeg skal oppnå det samme trykket må stempelet mitt være A = 637.432 / 294 200 = 0,0022 m². Jepp, det stemmer. Litt mindre så burde jeg ikke har noe problem med å løfte bilen.

 

Flyt og viskositet

Flyt i et hydraulisk system er bevegelsen av en mengde væske gjennom et punkt over en viss tid. Væsker er innelåst i slanger og rør i hydrauliske systemer, så flyt er væskens bevegelse gjennom disse.

Flyt (symbol Q) oppgis i liter per minutt (LPM) eller kubikkcentimeter per minutt (cm³/min) eller per sekund (cm³/sek).

Flyt = Areal (tverrsnitt) X Hastighet     (Q = A x V)

Det er viktig når dette regnes ut å bruke korrekt enhet og verdi på begge sider av ligningen; dersom arealet oppgis i cm² og hastigheten i m/sek må det gjøres om til cm/sek og resultatet blir i cm³/sek, osv...

Viskositet er "tykkelsen" til en væske og i hydrauliske systemer er lav viskositet ønskelig. Jo lavere viskositet en væske har, jo mindre energi kreves for at den skal endre form eller posisjon. En økning i viskositet i en væske vil øke tiden væsken bruker på å bevege seg fra punkt A til B med det samme trykket. Altså vil flyten synke.

Utregning av viskositet er et kapittel for seg selv og ikke rent ukomplisert, men det måles hovedsaklig i Pascal-sekunder, som, hvis jeg skal slakte definisjonen av, betyr at med et trykk på 1 Pa beveger væsken seg X meter på ett sekund. Alle væsker har positiv viskositet, null viskositet observeres kun i supervæsker ved svært lave temperaturer. Generelt sett er væsker regnet som viskose dersom de er betydelig tregere enn vann.

Yoghurt har høyere viskositet enn vann. Hadde du brukt yoghurt i et vanngevær ville det ikke skutt særlig langt.

 

Flyten i et hydraulisk system beskrives enten som laminar flyt eller turbulent flyt. Vi liker å tro at væske beveger seg i den retningen man dytter den uten større problemer, men væske er stort sett turbulent. Laminar flyt er god flyt og er ønskelig, men vanskelig å oppnå.

Det hjelper å ha avrundede kanter i systemet og unngå skarpe ≥ 90 grader retningsendringer.

For å beskrive punktet når en væske eller gass går fra å være laminar til turbulent etter at den kommer ut av "kilden" brukes noe som kalles Reynolds-nummer (Re), introdusert av Sir George Stokes, og popularisert av Osborne Reynolds.

 

Bernoulli's prinsipp, oppkalt etter Daniel Bernoulli, sier at; når hastigheten til en væske øker, synker trykket proporsjonalt. Se video under for demonstrasjon av fenomenet. Det er verdt å nevne at det er ikke teknisk sett et mediums hastighet som fører til en trykkendring, men hastighetsendringen i seg selv som fører til trykkendringen.

Når en væske beveger seg gjennom et system vil den opprettholde lik flyt. Så dersom den går fra et stort rør til et mindre, vil arealet synke, så for å opprettholde samme flyten må naturligvis hastigheten til væsken øke. Dette kalles kontinuitet og beskrives med:

Arealet ganger hastigheten i punkt 1 er lik arealet ganger hastigheten i punkt 2.

Når dette skjer synker trykket. Når væsken går fra et lite rør tilbake til et større rør skjer det motsatte, at hastigheten vil synke og trykket stige.

Dette er også kjent som Venturi-effekten som er en utnyttelse av Bernoulli’s prinsipp.

Bernoullis formel ser normalt sett slik ut:

bernoulli_formel.png

Formelen leses slik: Når flyten er konstant er trykket pluss massen ganger tyngdekraften ganger høyden over bakken pluss massen ganger hastigheten i annen delt på to lik i to ulike punkter i samme systemlinje.

 

 

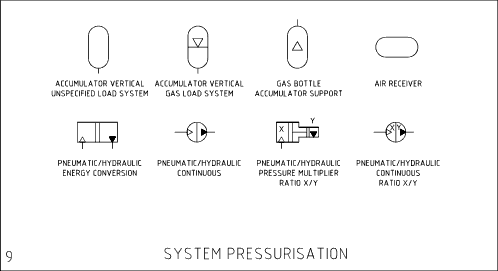
Trykk i komprimerbare systemer

Pneumatikk oppfører seg litt annerledes enn hydraulikk, siden gasser er komprimerbare.

Boyle's lov, oppkalt etter Robert Boyle, sier at; ved konstant temperatur er forholdet mellom trykk og volum konstant i et lukket system med komprimerbar gass. Altså, når volumet synker, øker trykket. Eller rettere sagt, i en trykkluftkompressor, nårru stapper mer luft inn i samme tanken fårru større trøkk.

Forholdet i Boyle's lov uttrykkes med: P x V = k der P er trykket og V er volumet og k er konstant.

Matematisk kan den brukes slik:

Eksempel på Boyle's lov og atmosfærisk trykk. Flasken ble fylt med luft høyt oppe der det atmosfæriske trykket er lavt og når den ble fraktet ned komprimerte det utvendig trykket volumet på beholderen for å utligne trykket og inni og utenfor.

 

 

I praksis, skjematikk og symboler

I bruk kan et enkelt hydraulisk system se slik ut:

  1. Hydraulisk olje

  2. Reservoar

  3. Filter

  4. Pumpe

  5. Flytretningskontroll

  6. Hydraulisk sylinder med stempel

  7. Linjer (rør eller slanger)

  8. Overtrykksventil

  9. Kjøler

Her representerer de rød linjene væske under trykk og de grønne representerer returlinjene.

Den hydrauliske sylinderen fungerer ved å kontrollere flytretningen til oljen slik at den blir presset inn foran eller bak stempelet slik at det blir produsert henholdsvis minusbevegelse og plussbevegelse, der stempelet går inn og ut respektivt. Pascal's prinsipper blir her observert ved den lille innløpsporten som er mye mindre enn overflaten til stempelet og mangedobler kraften.

Systemet over kan tegnes skjematisk slik:

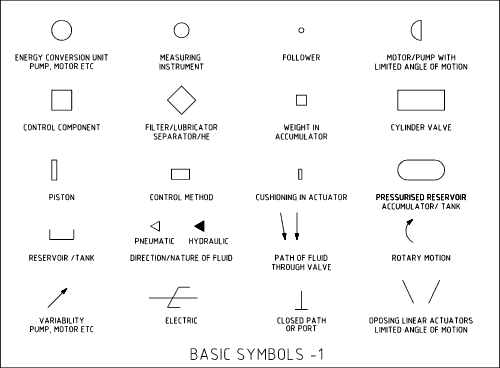
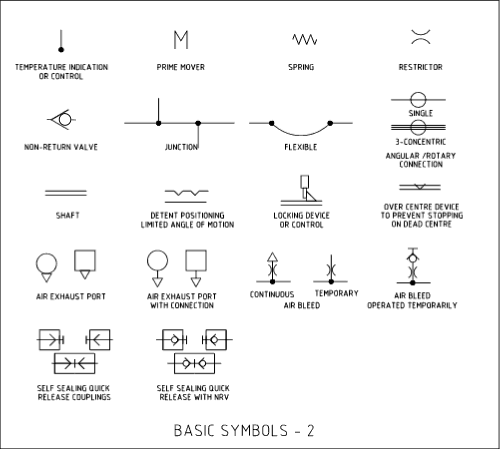
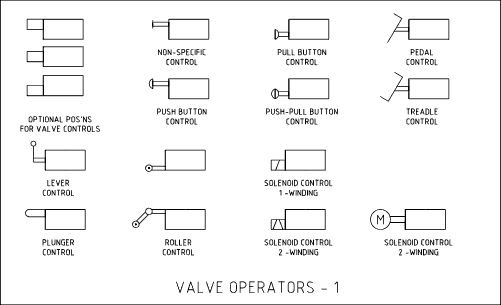
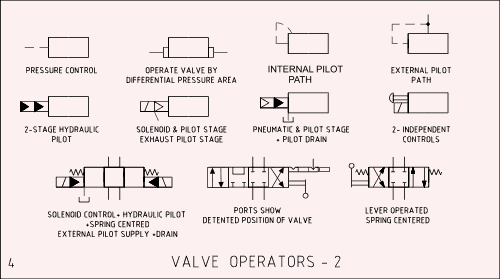
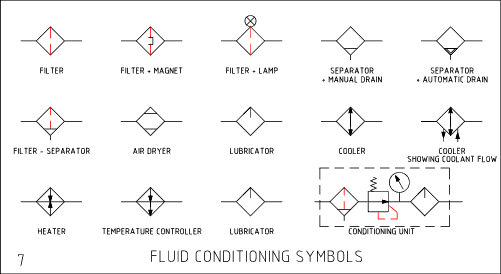
De skjematiske symbolene for hydraulikk og pneumatikk ble utviklet av ANSI og adoptert av ISO.

Skjematiske tegninger viser koblinger, flyt, og funksjon til komponenter. De indikerer ikke fysisk konstruksjon av komponenter eller verdier og trykk, posisjon av kontroller eller koblingspunkter. Symboler tegnes vanligvis i nøytral eller normal posisjon.

Typen drift og retningen på flyten indikeres med en liten trekant slik:

Systemlinjer som er koblet sammen og linjer som bare krysser hverandre er indikert slik:

Begge måter er riktig.

Andre grunnleggende symboler:

Korrosjon

/

Korrosjon er en fellesbetegnelse for reaksjonen (oksidasjon) som oppstår mellom metaller og luft og/eller vann eller en elektrolytt, som f.eks. saltvann.

Når man snakker om korrosjon er det vanligvis negativt; laget som danner seg på metaller og spiser det opp er ofte uønsket og er et stort problem generelt sett, men begrepet kan også brukes for å beskrive en ønsket reaksjon eller kontrollert korrosjon.

 

Kjemisk korrosjon

Når metaller kommer i kontakt med oksygen og hydrogen reagerer det ved å danne oksider, hydroksider eller sulfider. De fleste metaller ligger nogen lunde midt i det periodiske system og reagerer enkelt med andre stoffer. De "edle" metallene, bl.a. kobber, palladium, gull, sølv og platina, reagerer svært lite og meget sakte med omgivelsene og er de eneste metallene som finnes i ren form i naturen.

Ordet oksidasjon kommer fra oksygen og er reaksjonen som forekommer når oksygen kommer i kontakt med metaller.

Siden reaksjonen tar atomer fra metallet og luften/vannet og danner nye stoffer "spiser" dette opp metallet, og det nye stoffet, f.eks jernoksid, legger seg som et lag utenpå det opprinnelige metallet. Dette laget kalles gjerne rust, men det gjelder da kun i tilfellet til jern. Jern ruster og kobber irrer, alle andre metaller korroderer.

Når vi sier at noe ruster er det oftest snakk om overflatekorrosjon.  Dette er alminnelig korrosjon som legger seg jevnt over hele materialet (uniform korrosjon).

Punktkorrosjon eller "pitting" er korrosjon av enkelte deler og mindre områder på et materiale og kan være vanskelig å oppdage. Oppstår gjerne i hull eller sprekker i lakk og annen beskyttende etterbehandling.

Erosjonskorrosjon er korrosjon som kommer av bevegelse mellom metall og korroderende materiale, som foreksempel vann i rør eller metall som gnisser inntil andre ting som bidrar til at oksidlaget blir slipt bort som akselererer korrosjon av nytt metall under.

Stagneringskorrosjon er korrosjon som oppstår av akkumulering av fukt eller andre korroderende stoffer i områder hvor det har en tendens til å bli liggende lenge uten renne bort eller fordampe, som under skruehoder, pakninger eller i groper.

Andre faktorer som pH-verdi i miljøet rundt kan også påvirke korrosjonen.

 

Elektrokjemisk (galvanisk) korrosjon

Galvanisk korrosjon er korrosjon som oppstår mellom to ulike metaller som er i direkte kontakt eller elektrisk sammenkoblet med hverandre. Alle metaller har ulikt elektrisk potensiale, eller spenning, og reagerer kraftigere avhenging av hva slags metall det er i kontakt med.

Det beskriver i bunn og grunn hvilke metaller som er mest reaktive, eller gir fra seg elektroner lettest.

Som man kan se er sink og magnesium veldig reaktive, dvs. de slipper lett taket på elektronene sine hvis de blir bedt om det av et mer positivt metall, som f.eks. stål og fungerer som en anode og skaper positivt ladede ioner. Hadde man parret sink med et enda mer reaktivt metall ville sink blitt katoden.

Det er 3 betingelser for at galvanisk korrosjon skal finne sted:

  1. Metallene må være elektrokjemisk ulike
  2. De må ha en elektrisk forbindelse
  3. En elektrolytt, som f.eks. vann, må være tilstede mellom metallene

 

Enkelt om kjemien bak det

Som vi kan se på det periodiske system over er f.eks. helium helt til høyre og hydrogen helt til venstre. Atomnummeret beskriver antallet protoner og nøytroner atomet har, og i en normal nøytral form har atomet like mange mange elektroner som protoner.

Atomer har flere "skall" med elektroner, noe som kategoriseres med elektron-konfigurasjonen. Atomer kan ha maksimalt 2 elektroner i det innerste skallet, deretter 8, så 18 i det tredje, deretter 32, 50, 72. Et lag må ikke nødvendigvis være fullt før elektroner kan samle seg i det neste. Gull har for eksempel elektronkonfigurasjon 2-8-18-32-18-1.

Atomer med fulle skall reagerer ikke med andre stoffer, f.eks. edelgassene helt til høyre. Alkaliske metaller helt til venstre har et elektron "for mye" så de binder seg gjerne med andre stoffer eller kvitter seg gladelig med elektronet sitt.

Dette skulle tilsi at gull er svært reaktivt, og det er reaktivt, men på en langt langt mindre skala enn man skulle tro. Årsaken til dette er komplisert, men elektronene er pakket så godt sammen at de ikke vil gi slipp på hverandre, inkludert det ytterste, og beveger seg så fort at andre elementer har vanskeligheter med å binde seg til gull. Men nok om det.

Dersom et atom har ulikt antall elektroner som protoner bærer det en ladning og kalles et ion. Atomer med flere elektroner enn protoner er negativt ladet og kalles et anion. Atomer med flere protoner enn elektroner er positivt ladet og kalles et kation. Derav navnene "anode" og "katode". Dette er litt forvirrende ettersom elektrodenes ladning endres når vi tilfører strøm eller trekker ut strøm, som er forskjellen på en galvanisk celle og en elektrolytisk celle. Dette er litt utenfor behovet av kunnskap om galvanisk korrosjon, men en galvanisk celle er i bunn og grunn et batteri og en elektrolytisk celle er mye brukt i forkromming (electroplating) og andre industriprosesser hvor man legger et lag av et metall utenpå et annet.

I en galvanisk celle er det to reaksjoner som finner sted samtidig, reduksjon og oksidasjon. Sammen skaper de en redoks-reaksjon som er en sammenslåing av de to ordene. Stoffer som blir redusert MOTTAR elektroner (katoden) og stoffer som blir oksidert MISTER elektroner (anoden). Det er litt omvendt av det man skulle tro, og det henger igjen fra gammelt av før vi visste bedre, slik mye gjør, men det er nå engang slik.

I eksempelet om elektrolytisk behandling til venstre tilfører man positiv spenning og "drar" elektroner ut av sølvet(+) som da har mer lyst til å binde seg til oksygenet i elektrolytten og skaper positive ioner (siden de nå mangler elektroner) og flyter bort til skjeen av stål (-) hvor de gjenforenes med sine tapte elektroner som har tatt veien gjennom batteriet og legger seg som sølv på utsiden av stålskjeen. Vi tvinger dette til å skje ved å tilføre spenningen. Hadde det ikke vært noen ekstern spenningskilde ville skjeen rustet siden sølv er mindre reaktivt enn stål og hele prosessen ville forekommet i revers.

Det er relativt enkle kjemiske formler og kalkuleringer inne i bildet her for å beskrive redoks-reaksjoner, halv-reaksjoner, ionisering, oksidasjonstall og slikt, men det er ikke noe jeg sikter på å ta for meg for øyeblikket.

 

Beskyttelse mot korrosjon

Korrosjon og hindringen av det er et eget fagfelt og det er mange måter å utsette eller stanse korrosjon helt.

For eksempel er det vanlig å "skape" galvanisk korrosjon i maritime miljøer for å beskytte stål og andre lett normalt kjemisk korrosive materialer ved å skru fast biter med mer reaktive metaller for at disse skal korrodere før stålet. Vi ofrer et metall for å redde et annet, derav navnet "offeranode". Offeranoder er svært utbredt i skips- og offshoreindustrien for å beskytte skrog og platformbein og lignende.

Offeranoder er vanligvis laget av sink siden det er et av de aller mest reaktive metallene og er kost-effektivt. Disse må byttes ut jevnlig for å opprettholde den galvaniske beskyttelsen.

Galvanisk beskyttelse brukes ikke bare offshore og er svært utbredt i all industri. Galvanisering, som forresten har sitt navn fra den italienske vitenskapsmannen Luigi Galvani, men det var Alessandro Volta som gav det navnet.

Galvanisering brukes til å beskytte det meste. Spiker, skruer, plater, bjelker og mye annet innen bygg og industri.

Varmbads-galvanisering er mest utbredt hvor man rett og slett dypper ting i flytende sink som gir det et beskyttende lag. Først og fremst beskytter det stålet under som om det skulle være malt, men dersom galvaniseringen skulle bli skadet vil sinken fortsette å beskytte stålet via planlagt galvanisk korrosjon.

Metoder for å forhindre uønsket galvanisk korrosjon er blant annet å elektrisk isolere metallene hvis ulike metaller benyttes, ved f.eks. bruk av plastikk/gummi skiver rundt bolter og lignende. Det er anbefalt å ikke overstige en spenningsforskjell på 0,2V når materialer som skal være i elektrisk kontakt skal brukes.

Andre måter å beskytte mot rust innebærer å lage spesielle legeringer (blandinger av forskjellige metaller) som kan gjøre materialet mer beskyttet mot korrosjon.

Utover det er det veldig vanlig å dekke metallet med en eller annen form for tett lag som hindrer luft og fukt fra å komme i kontakt med metallet under. Maling, lakk, blånering, parkerisering, innsmøring med olje eller fett er alle måter å forhindre korrosjon.

Som man kan se på spenningsrekken er aluminium et svært reaktivt metall, men det er kjent for å ikke korrodere...? Dette kommer av at aluminium reagerer raskt med oksygenet og danner aluminiumoksid, som binder seg tett og dypt med aluminiumet under og danner et naturlig beskyttende lag. Av denne grunnen er aluminium også populært i maritime miljøer. Denne egenskapen er for øvrig mye brukt i industrien til ikke bare å beskytte aluminium-produkter mot korrosjon, men også bruke elektrokjemiens vidunderlige verden til å anodisere metaller for å gi dem spreke farger.

Parallellklemme

/

Etter å ha holdt på i flere måneder er jeg endelig ferdig med parallellklemmen jeg fikk som ekstraoppgave. Det er flere grunner til at det tok så langtid. For det første var det en omfattende oppgave med mange ulike prosesser, noen som jeg måtte lære meg før jeg kunne fortsette. For det andre så har jeg mye annet å holde på med og det har rett og slett ikke vært nok dager med verksted-tid til å bli ferdig.

Men nå er jeg endelig ferdig og kan fortelle litt om veien dit.

Jeg begynte med et stykke 20x20mm stål som jeg planfreste ned til 18x18mm. Toleransene mine var på 0,1mm, men jeg forsøkte som jeg ofte gjør å se hvor nøyaktig jeg kunne få det.

Jeg spente det opp i stikken og freste den ene siden rett, deretter vred jeg stykket 90° og freste den neste siden. Jeg brukte så disse sidene som referansesider da jeg freste de to andre sidene og dermed hele biten ned til korrekt tykkelse. Jeg var i stand til å oppnå en presisjon på +/- 0,02mm her, og det er jeg ganske fornøyd med.

Planfresen gav ikke en fin overflate, så jeg byttet ut de fem skjærene som viste seg å være ganske slitne og senket matehastigheten til litt over halvparten av det den stod på. Så vidt jeg husker benyttet jeg omdreiningstall på rundt 1000 r/min og matehastighet på ca. 250 mm/min. Dette gav en pen overflatefinhet.

Jeg målte så rettheten og parallelliteten og kom frem til at stykket er litt vridd, men det er innenfor toleranser så det gjør ikke noe. Tall på stykket er hundredeler. Stykket skal uansett deles i to, så da blir ujevnhetene "halvert".

Men før jeg kunne begynne med fresingen jeg gjorde i bildene over måtte jeg reparere fresen, eller rettere sagt det digitale avlesersystemet. Det var i ustand og gav ikke pålitelige utslag.

Skruene til sleide-festet var brukket og avleseren som skal sitte statisk på fresen var løs, samt at sleiden på aksebordet var slarkete, så vi tok av alt, renset det og byttet ut skruene.

Mye bedre.

Deretter kappet jeg arbeidsstykket i to og freste sidene like.

Jeg freste dem her ned til korrekt lengde, dvs. 110mm, med ganske imponerende +/-0,01 mm avvik. I etterpåklokskapens navn hadde det vært en fordel å la det være igjen litt materiale siden endene skulle files runde, men det endte opp med å ikke bli et stort problem.

Da stykkene var innenfor korrekte dimensjoner brukte jeg høyderissemåler, rissepenn, linjal og skyvelære for å risse dato- og reveranselinjer.

Med hovedfreseoperasjonene utført filte jeg endene runde. Jeg grovslipte stykkene med slipemaskin og gjorde resten med flatfil og smergel.

Jeg sjekket ofte med radielære og passet på å holde filen rett. Jeg brukte også filen med smergel i mellom for å få en solid flate mot stykket slik at ikke kantene ble ulikt slitt i forhold til midt på stykket som kan oppstå dersom man bruker smergel for seg selv siden det kan strekke seg.

Deretter kom en litt komplisert operasjon. Andre enden av stykkene skal ha en 22,2° vinkel. Her brukte jeg en ganske nøyaktig vinkelmåler for grovkappet.

Jeg hadde allerede risset referanselinjer, så jeg visste hvor vinkelen skulle starte og stoppe på de to sidene. Da jeg kom nærme målene freste jeg ned til jeg nådde en av de to referanselinjene, enten den på toppen eller den på enden og vinklet stykket litt anderledes. Jeg brukte den siden som var korrekt til å rekalibrere fresehodet og gjorde et kutt for å teste vinkelen. Var det enda litt å gå på banket jeg forsiktig på stykket for å endre vinkelen og rekalibrerte stykket igjen for så å ta et nytt kutt. Det finnes nok en mer eksakt måte å gjøre det på, men vi har ikke skrustikker som kan vinkles i 2 akser, så da måtte jeg gjøre det manuelt. Jeg kunne også vinklet selve fresehodet, noe jeg gjør i en senere operasjon, men det hadde blitt enda mer arbeid å få korrekt vinkel.

Jeg ble ganske fornøyd med resultatet.

Jeg boret hull i stykkene som skruene skal gå gjennom og gjenget disse med M10 gjengtapper.

Her benyttet jeg en pinol/senterspiss for å påse at gjengetappen sto rett. Det fungerte veldig bra.

DSC_0943.jpg

Når det er sagt så ble ikke hullene helt korrekt overfor hverandre. Jeg hadde stykkene oppå hverandre i stikken i søylebormaskinen slik at hullene skulle bli på nøyaktig samme sted. 

Men boringen min var tydeligvis litt ute av senter og jeg hadde dem plassert SAMME VEI slik at når jeg snudde det ene stykket rundt får å skru dem sammen ble feilen åpenbar... Så jeg lagde to nye stykker.

Det var ergerlig å starte så godt som helt på nytt, men jeg kunne ikke leve med slikt slett arbeid hengende over meg.

Denne gangen var jeg ekstra nøye med plasseringen av hullene og jeg boret de to stykkene hver for seg. Da ble det bra.

De vinklede endene skulle files runde med en radius på 5mm. Personlig syns jeg det ser bedre ut som det gjør, men jeg fulgte tegningene.

Det eneste som da gjensto å gjøre med selve klemmene var å frese V-sporet som skal holde klemmen sentrert og gi bedre grep om det som klemmes sammen, samt de skrå sporene på sidene.

For å frese V-sporet brukte jeg en 3mm pinnefres med en collet-kjoks og vinklet fresehodet 45°.

For å vinkle fresehodet løsnet jeg de fire boltene som holder det fast som på bildet under.

Jeg byttet ut fresekjoksen til en collet kjoks. Colleter, eller halser, er utbyttbare kjoksstykker med ulike indre diameter for å sette fast mange typer verktøy eller arbeidsstykker. Når man strammer kjoksen presses colleten sammen og griper og sentrerer verktøyet.

For å bytte collet-holderen skrur vi ut trekkstangen som går gjennom fresehodet ved å skru opp mutteren som strammer den på toppen.

Deretter setter vi inn pinnefresen og strammer med kjoksnøkkelen.

Pinnefresen stakk litt langt ut, men det måtte bli sånn for at kjokshodet skulle gå klar av arbeidsstykket.

V-sporet skulle være 3mm bredt, som vil si at med en 45° vinkel blir kuttet 1,5mm dypt. Jeg freste opp sporene i flere passeringer for ikke å skade pinnefresen siden den var så liten og stakk så langt ut.

På sidene brukte jeg en 4mm pinnefres siden enderadiusen på sporet skulle være 2mm. For å frese disse sidene måtte jeg bruke midten av pinnefresen, som fungerte greit, men ikke optimalt. Hadde jeg hatt V-blokker hadde jeg spent opp stykket anderledes for å kunne heve stykket loddrett opp i fresen i endene for å lage et renere kutt, men etter litt opprensking med fil ble resultatet helt OK.

Skruene var relativt enkle å lage, men det å dreie gjengene var noe jeg måtte lære meg for dette prosjektet og det var en liten utfordring, men det ble gjenger av det til slutt og hvordan har jeg dekket i mitt forrige innlegg.

Jeg dreide så tynne ting at hardmetallskjæret til dreiebenken ikke kunne brukes siden benken ikke går fort nok til å oppnå riktig skjærehastighet. Så jeg slipte mitt eget hurtigstålskjær.

Jeg forsøkte å bruke litt kjølevæske på en mer... manuell måte og resultatet ble forsåvidt greit, men det var ikke verdt bryet, spesielt med tanke på at hodet skal serrateres og resten gjenges.

Jeg serraterte med toppsleiden og meget lav matehastighet med trykkluft som blåste ut sponet. Da ble resultatet meget bedre enn tidligere forsøk.

Jeg slipte et nytt formskjær, 3mm bredt med en radius på 1,5, i hurtigstål for å kutte frisporene til gjengene.

Deretter avfaset jeg endene.

Til slutt dreiet jeg gjengene

Badabing badabom, det tok sin tid, men jeg har lært masse.

Og ikke det at jeg ikke visste dette fra før, men dette prosjektet har virkelig gitt meg viktig lærdom:

Stopp. Tenk. Tenk litt mer. Utfør.

Gjenger og hvordan å dreie dem

/

Skruer binder verden sammen på en enestående måte og dreiing av gjenger er en av de mest utførte maskineringsprosesser i verden, på en årlig basis, så å kunne dreie gjenger ordentlig er viktig kunnskap.

Den tekniske definisjonen på en maskinskrue er et skråplan viklet om en sylinder. Gjenger er altså en opphøyning eller nedfelling av en profil i form av en heliks på den interne eller eksterne overflaten av en sylinder.

For å forstå hvordan vi lager dem må vi forstå hvordan de fungerer og standardene som er i bruk. Desverre er det mer enn én standard, som i seg selv bekjemper formålet med standarder, men det er som det er.

Arkimedes' skrue

De to store enhetsystemene og standardene som bruker dem.

SI - Système international d'unités

Det metriske system og det som blir mest brukt blant forskere og i den vitenskapelige verden. Det som gir mening.

Imperial - British Imperial / Exchequer Standards

Det imperiske enhetsystem som blir offisielt brukt av Libera, Myanmar og USA. Det som ikke gir mening.

 

 

 

ISO - International Organization for Standardization

Etablert i 1927 og holder til i Genève, Sveits. Et konglomerat av alle medlemsnasjonene sine interne standardiserings-organ.

Bruker SI metrisk som hovedstandard, men omfatter også Amerikanske enheter siden dette er en internasjonal gruppe.

ISO har standarder for ALT mulig, ikke bare industri, som for eksempel ISO 8601 som beskriver hvordan man skal skrive tid og dato. Det korrekte formatet er forresten 2017-03-29T23:59:59+01. Så vet du det.

 

DIN - Deutsches Institut für Normung

Blandt annet ansvarlig for mye av moderne bilstandarder, som for eksempel form på bilstereo (1-DIN / 2-DIN) o.s.v.

Viktig ISO medlem og bruker SI enheter.

CEN/EN - European Committee for Standardization / European Standard

EU sitt interne organ for standarder som opererer mye på samme måte som ISO. Hvorfor de har sitt eget når vi har ISO er et godt spørsmål. Norge er medlem i både CEN og ISO.

 

ANSI - American National Standards Institute

De forente staters standardiserings-organ.

De omhandler både metrisk og imperisk, men bruker offisielt metrisk som hovedsystem, men det går for det meste i tommer fortsatt.

BSI Group - British Standards Institution

Storbritannia sitt standardiserings-organ.

Viktig medlem av ISO og CEN. Er på samme måte som USA offisielt sett gått over til metrisk, men i motsetning til sine frigjorte brødre faktisk flinke til å implementere det.

 

NS - Norsk Standard / Standards Norway

Norges offisielle standardiserings-organ.

De har ikke noen kul logo.

Hvis du ser NS-EN så står EN for “Europeisk Norm” og betyr at standarden er adoptert fra ISO/CEN, men kan i andre sammenhenger bety "Engineering Number" og er en standardisert nummerering av materialer.

“Great things happen when the world agrees.”
— ISO

Gjengestandarder

Som sagt, det å ha mer enn en standard for samme tingen motarbeider formålet med standarder.

De to hovedstandardene når det kommer til gjenger er Metric (M) og Unified (UTS). Metrisk er ISO standard, Unified Thread Standard er hovedsaklig brukt i USA og Canada og styres av ANSI.

Begge standardene bruker 60° V-gjenger, men hovedforskjellen ligger i måleenhetene og gjengemålingen.

Mye på samme måte som tannhjul måles stigningen i det Metriske system med avstanden mellom et punkt på en gjenge og det samme punktet på neste gjenge parallelt med aksen.

Metrisk standard deles i to grupper, metrisk grovgjenger, enkelt kalt M, og metrisk fingjenger, noen ganger kalt MF for Metric Fine.

Alle mål i metrisk gjengestandard oppgis i millimeter. Metriske grovgjenger uttrykkes ved å sløyfe stigningen, f.eks. M14. Dersom det står M14 x 1.5 betyr det at det er metriske fingjenger.

I Unified måles gjengestigningen med hvor mange gjenger som går på en tomme. Dette medfører problemer siden antallet gjenger over en tomme ikke nødvendigvis er et rundt tall, f.eks. 16,5 TPI.

UTS deles i tre grupper, UNC (Unified Coarse), UNF (Unified Fine) og UNEF (Unified Extra Fine).

Mål i UTS er en skikkelig godtepose full av rariteter. Noen ganger oppgis det i brøkdeler av en tomme, noen ganger desimale fraksjoner (0.1120), noen ganger kun som et nummer, f.eks. #4.

 

Gjengeprofiler

Det finnes mange ulike typer gjengeformer og man kan bruke en hvilken som helst form på gjenger så lenge de korresponderer i delene som skal sammenføyes.

De vanligste gjengeprofilene er som følger:

  • a) Standard utrimmet 60° V-gjenger

  • b) ISO metriske 60° V-gjenger, den vanligste gjengformen. Gir stor friksjon og sitter godt.

  • c) Withworth 55° gjenger, mye brukt der man bruker tommer.

  • d) Firkantgjenger, gir veldig lav friksjon og tåler høy last, men vanskelig å produsere. Ofte brukt i ledeskruer i industrimaskiner.

  • e) Trapesgjenger (også kjent som Acme-gjenger). Gir lav friksjon og tåler høy last. Lett å produsere. Brukes også i ledeskruer.

  • f) Buttress-gjenger, brukes som ledeskruer, låseskruer eller tetningskruer i hydraulikk.

  • g) Runde gjenger, gir relativt lav friksjon og brukes mye i ting som skal være lette å skru ut og inn, som lyspærer eller på rørtenger osv.

 

Gjengens anatomi

Ved dreiing av eksterne gjenger (bolter o.l.) er det storediameteren som er viktig, dvs. den ytre diameteren, som er den som oppgis i standardene. M14 bolter er 14mm tykke... teoretisk sett, i realiteten er de gjerne 13,97- 13,79 millimeter for å tillate litt toleranse mellom eksterne og interne gjenger, det er standarder for dette også.

Lillediameter eller indre diameter beskriver dybden på gjengene og representerer roten i eksterne gjenger og toppen i interne gjenger.

Som man kan se på tegningen over er det rot og toppklaring bygget inn i gjengene. Den egentlige størrelsen måles med de teoretiske toppene. Toppklaringen er 1/8 av stigningen og rotklaringen er det dobbelte på 1/4 av stigningen. Disse er omvendt for interne gjenger. H er den teoretiske høyden på gjengene fra spiss til spiss, Harb (arbeidshøyde) kan brukes for den faktiske høyden mellom rot og topp. P står for "pitch" og er stigningen og måles på delediameteren, men kan praktiske sett måles hvor som helst på gjengene.

Forholdet mellom stigning og gjengedybde er grunnen til at 60° gjenger er standard:

400px-ISO_and_UTS_Thread_Dimensions.svg.png

Vinklene i en trekant blir alltid 180°.

I en likesidet trekant er alle vinklene 60° og alle sidene er like lange.

Høyden, dvs. lengden på normalen fra siden som går gjennom et hjørne har et fast forhold i en likesidet trekant:

Dette kommer av Pytagoras' teorem som sier at A² + B² = C².

Dette gir også at C² - A² = B², altså høyden.

Som et eksempel la oss si at stigningen er 6mm, altså lengden av èn side:

I praksis

Det er hovedsaklig to måter å dreie gjenger på. Med toppsleiden, eller med tverrsleiden. Den "korrekte" måten er med toppsleiden.

Med informasjonen over i tankene kan vi sette i gang å dreie gjenger. Jeg tar her hovedsaklig for meg dreiing av eksterne gjenger, men prinsippene ved dreiing av interne gjenger er de samme.

Først setter vi dreiebenken til riktig stigning. Når hovedsleiden blir koblet til ledeskruen beveger den seg X antall millimeter bortover for hver rotasjon av kjoksen, der X er stigningen til gjengene vi skal dreie.

Det er viktig å sørge for at maskinen står stilt inn på riktig standard.

Vi setter toppsleiden til 29,5°, altså litt under halvparten av flankevinkelen. Dette er for å skjære spon av arbeidsstykket på en mer kontrollert, presis og finere måte.

Dreieskjæret er et formverktøy og har samme vinkel som gjengene, 60°.

Tverrsleiden står alltid på null og brukes som referansepunkt.

Kuttdybden økes med toppsleiden. Når toppsleiden brukes til å øke kuttdybden kan vi gå inn hele stigningnen med toppsleiden siden den står vinklet slik at å mate den inn hele stigningen resulterer i en total kuttdybde på 0,86603 ganger stigningen.

Det er viktig at skjæret står rett mot arbeidsstykket, dette kan verifiseres med et enkelt vinkelmål som i bildet under.

Vi starter med å gjøre en veldig liten passering for å verifisere med gjengelære at maskinen er stilt inn riktig og at gjengene blir som vi ønsker.

Deretter tar vi ganske mange passeringer, gjerne 5 - 16 passeringer, avhenging av stigningen. Siden matehastigheten på hovedsleiden er såpass stor når vi dreier gjenger er det nødvendig å dreie med lavt turtall, men som med vanlig dreiing blir resultatet bedre jo nærmere optimal skjærehastighet vi er.

Det er vanlig å ha et frispor i enden av gjengene om dette tillates for å gi skjæret et trygt sted å stoppe og gi et pusterom til operatøren slik at skjæret trygt kan trekkes tilbake ut av veien fra arbeidsstykket.

Når hovedsleiden er engasjert i ledeskruen er det som regel ikke å anbefale å koble den fra, men heller reversere maskinen for å komme tilbake til start. Det er også viktig å ikke røre hovedsleiderattet for å ikke introdusere slark i ledeskruen og endre referansepunktet til gjengeskjæret.

Dersom dreiebenken har en gjengeklokke kan dette gjøres, men da er det viktig at ledeskruen kobles til ved den samme indikasjonen på klokken hver gang.

Dersom man dreier noe mer fler enn en gjengeinngang kan man enten bruke gjengeklokken til å forskyve gjengesporet, eller sette toppsleiden 90° og benytte den til å forskyve gjengene.

Dette har også andre formål, som f.eks. en alternativ måte å øke kuttdybden på ved å alternere hvilken side som kuttes, dog dette gjøres for det meste i CNC maskiner og er ikke en utbredt praksis ved manuell dreiing.

Helt til slutt en veldig god video om dreiing av gjenger som oppsummerer det som står her veldig godt:

Driv verden fremover, bruk ISO <3

Gir og utveksling

/

Vet du hvorfor det er så mye olje under havbunnen? Jo for den smører jordaksen. Og hvis vi pumper opp all oljen vil jorda slutte å snurre. Så hvorfor pumper vi opp oljen? Oppfinnelsen av hjulet, som mye av oljen i dag driver rundt, blir betraktet som den første og mest innflytelsesrike oppdagelsen i menneskets historie, og da man lagde dem av metall og puttet tenner på det var tiden inne for maskinalderen.

Tannhjul driver verden fremover med sin trofaste sirkulære og repeterende bevegelse. Ikke-sirkulære tannhjul eksisterer også, men de er brukt i svært spesielle situasjoner. Tannhjul er som navnet tilsier hjul med tenner som overfører mekanisk kraft fra en aksel til en annen.

Utveksling er det som forekommer når ulike tannhjul settes i bruk sammen og driver eller drives rundt. Utveksling er en fundamental teknisk egenskap i maskineri og er grunnen til at vi kan lage maskiner som gjør det de gjør på en effektiv måte. Vi finner utveksling overalt rundt oss, i biler, sykler, kjøkkenmaskiner, verktøy, etc.

Selve grunnprinsippet er relativt enkelt; Et mindre tannhjul som driver et større tannhjul gir mer kraft, men mindre fart. Et større tannhjul som driver et mindre ett gir større fart, men mindre kraft. Partall antall tannhjul gir en endring i retning, mens oddetall antall gir den samme retningen som drivhjulet.

Tannhjul i inngrep er i bunn og grunn konstant roterende eksempler på Newton's tredje lov, om kraft og motkraft.

“Every action has an equal and opposite reaction.”
— Isaac Newton

Jo større tannhjulet er, jo lenger tennene er fra senter, jo lettere er det å snurre det. Kraft ganger arm og alt det der. Derfor er det lettere for et mindre tannhjul å drive et større og omvendt.

 

Giret som tilfører kraften i systemet blir kalt det drivende hjulet (eng: driver) og det tilkoblede hjulet blir kalt det drevne (eng: driven).

For å få samme rotasjonsretning på det drevne tannhjulet må et ekstra hjul tilføres mellom det drivende og det drevne hjulet. Dette kalles et reverseringshjul (eng: idler gear) fordi det kun eksisterer for endre retningen på det drevne hjulet.

Det går derfor ikke an å sette 3 tannhjul direkte sammen slik som (desverre) ofte blir brukt i logoer som denne:

Her har det gått helt rundt for noen.

Her har det gått helt rundt for noen.

 

Utvekslingsforhold

Utvekslingsforhold (eng: gear ratio) er forholdet mellom tanntallet eller diameteren på to tannhjul og ved reim- eller kjededrift. Utvekslingsforhold uttrykkes på samme måte som målestokk, f.eks. 1:5 (en til fem). Det første tallet representerer det drivende hjulet og det siste representerer det drevne.

Forholdet kan også uttrykkes som brøk 1/2 og 2/1 eller heltall/desimaltall 0,5 eller 2 der tallet representerer hvor mange ganger det drivende hjulet går rundt per revolusjon av det drevne

For å beregne utveksling deler vi tanntallet til det drevne hjulet på tanntallet til det drivende. Tanntallet er antall tenner på tannhjulet.

Utvekslingsforholdet kan beregnes med formelen:

Et tannhjul med 10 tenner.

Et tannhjul med 10 tenner.

Merk at ved beregning med omdreiningshastighetene skal det drivende deles på det drevne, i motsetning til de to andre formlene der det drevne deles på det drivende. Dette er fordi tanntallet og diameteren er direkte omvendt proporsjonal med hastigheten. Mer tenner = lavere hastighet og vice versa.

Denne formelen gir også for eksempel at:

Z kan også erstattes med D o.s.v.

Disse formlene gjelder for alle typer tannhjul; sylindriske, heliske, koniske og snekkeskruer.

I eksempelet over går det drevne tannhjulet B 1 og 1/2 gang rundt for hver revolusjon av det drivende A. Vi kan skrive at utvekslingsforholdet er 1:1,5 men det ser ikke særlig pent ut. Vi bør heller skrive 2:3. Så hvor mange tenner har da A hvis B har f.eks. 20?

Først gjør vi om tanntallet til B og utvekslingsforholdet til brøk. Deretter deler vi tanntallet på forholdet ved å snu den bakerste brøken og gange som vanlig. Av det får vi et pent svar. Dersom vi får et desimalsvar er det noe som er feil. Vi kan ikke ha f.eks. 30,6 tenner på et tannhjul.

 

Sammensatte tannhjulssystemer

Med ett sett med tannhjul kan vi lage en hvilken som helst utveksling, men ved svært store utvekslinger blir enten det ene tannhjulet svært lite og vil ikke rotere ordentlig, eller det andre blir alt for stort til å være praktisk. Eller begge deler.

Derfor kan vi sette to tannhjul på den samme akselen og dermed lage et sammensatt tannhjulsystem (eng: compound gear train).

På illustrasjonen over er tannhjul B og C koblet sammen slik at de roterer med samme hastighet. Tannhjul A og B er i inngrep og tannhjul C og D er i inngrep. Dette skaper to utvekslingsforhold og systemets totale utveksling kalkuleres ved å multiplisere de to utvekslingene.

A = 36 tenner   B = 18 tenner   C = 32 tenner   D = 16 tenner

Så hvordan regner vi andre veien? Si at vi har en utveksling på 24:1 som vi vil oppnå med så små tannhjul som mulig, men intet tannhjul skal være mindre enn 8 tenner. Vi kan gange begge sider med 8 å få 192/8 tenner som tilfredsstiller kravet til det lille tannhjulet men det drevne tannhjulet vil bli veldig stort.

24 kan faktoreres til 4x6 så vi kan lage en utveksling som gir 4:1 og en som gir 6:1. Ganger vi så dette med kravet om det minste tannhjulets tanntall, 8, får vi 32/8 tenner og 48/8 tenner som gir oss samme reduksjonen, men med totalt tanntall i systemet på 96 istedenfor 200 med mye mer kompakt konstruksjon. Dette kan gjøres enda mer kompakt ved å innføre enda et ledd i systemet som gir oss faktoren 2 x 3 x 4.

Mer informasjon i videoen under:

 

Snekkedrift

Reduksjoner med vanlige sylindriske tannhjul holdes normalt sett til ikke større enn 10:1. Dersom virkelig store utvekslinger kreves kan vi benytte snekkedrift som vanligvis benyttes mellom 10:1 og 500:1 reduksjoner.

Snekkedrift (eng: worm drive) eller skruehjulsdrift er drift der den tilførte kraften driver en skrue (eng: worm / worm gear) som er i inngrep med et tannhjul (eng: worm wheel) hvis aksel står 90 grader i forhold til drivskuren.

Snekkedrift brukes når svært stor utveksling kreves og er bygget på en måte slik at systemet selv-låser, det vil si at man kan bare tilføre kraft til skruen og når skruen ikke roterer vil hjulet ikke kunne rotere. Det er låst fast i gjengene på skruen.

Det finnes systemer der gjengene på snekkeskruen er vinklet slik at hjulet KAN drive skruen rundt, men dette medfører stor friksjon i systemet. Dette kalles omvendt snekkedrift.

På grunn av systemets selv-låsende natur egner det seg godt til f.eks. gitarer og andre strengeinstrumenter eller heisemekanismer.

Kalkulering av utveksling i skruehjulsystemer er nokså lik som normal utregning, men utvekslingen er antall tenner på snekkehjulet delt på antall gjengeinnganger på snekkeskruen (enkeltgjenget, dobbeltgjenget, trippelgjenget, o.s.v. ) Siden komponentene i systemet ikke opererer på samme måte kan vi ikke kalkulere utvekslingen ved delediameterne.

snekkedrift.png

Dette er fordi én rotasjon av snekkeskruen forskyver snekkehjulet kun én tannfordeling, per gjengeinngang på snekkeskruen. En tregjenget skrue vil flytte hjulet 3 tanndelinger per rotasjon.

Lead_and_pitch_in_screws_norsk.png

Skruehjulsystemer er designet slik at skruen og hjulet passer svært godt sammen, d.v.s. at tennene på snekkehjulet ofte er litt skråvendte får å passe gjengestigningen på skruen, samt at midten av tennene og tannbunnene er konkave for at skruen skal få så godt inngrep som mulig.

 

Koniske tannhjul

Dersom man ønsker å overføre kraft mellom to kryssende akslinger kan man benytte koniske tannhjul (eng: bevel gears).

Koniske tannhjul overfører kraft i en vinkel, og så lenge tuppen på de imaginære kjeglene møtes i samme toppunkt (eng: apex) kan man lage spisse, rette eller stumpe vinkler.

Tannhjulenes vinkel bestemmes av utvekslingsforholdet og tanntallet, og dersom en annen utveksling eller vinkel ønskes må begge tannhjulene byttes ut.

Den aller vanligste vinkelen er 90° og dersom tanntallet på de to tannhjulene er like kan dette på engelsk kalles "miter gears".

Det drivende hjulet i et tannhjulsystem kalles ofte "pinjong" (eng: pinion), spesielt i vinkeldrev der det drivende er mindre enn det drevne.

Vinkelen mellom akslingene er lik halvparten av de to kjeglevinklene.

34.png

Dette gir også at dersom man har en satt akselvinkel må summen av tannhjulenes konvinkel bli det dobbelte av akselvinkelen.

 

Heliske-, spiral-, og hypoid-tannhjul

En heliks er en kurve langs en sylinder eller kjegle som roterer rundt et punkt og øker i høyde med en konstant vinkel.

Lengden av en rotasjon av heliksen er lik hypotenusen av omkretsen og høyden mellom to korresponderende punkter på sylinderen (pitch).

Heliske tannhjul er tannhjul der tannprofilen er kuttet skrått over dybden av tannhjulet. Dette gir økt total kontaktflate og bidrar til stillere og sterkere gang. Kalkulering av utveksling med heliske tannhjul fungerer som normalt.

To heliske tannhjul i inngrep må ha motsatt heliksvinkel (høyrehendt og venstrehendt)!

Siden tennene er vinklet skaper heliske tannhjul aksial motstand som bør tas hensyn til ved f.eks. å introdusere aksiale kulelagere.

Dette kan også motvirkes ved å lage dobbelt heliske tannhjul eller fiskebein tannhjul.

Spiraltannhjul er tannhjul der tennene er skåret ut fra en spiral med startpunkt i senter av tannhjulet. Disse gir enda mykere og stillere gang enn heliske tannhjul, men med mer friksjon. Det finnes flere forskjellige varianter av spiraler i bruk.

Spiralskårne tenner brukes som regel bare på koniske tannhjul.

"Zerol" tenner er tenner skårne etter en sirkel hvis senterpunkt er på tangenten til det koniske tannhjulets delesirkel med radius lik tannhjulets halve delesirkeldiameter og tangenten lik denne radius.

Kalkulering av utveksling med spiraltannhjul fungerer som normalt.

Hypoidtannhjul er koniske tannhjul der pinjongen ikke er på linje med kronhjulets senter.

"Hypo" er gresk og betyr 'under'.

Hypoidtannhjul kan oppnå enda større utvekslinger enn tradisjonelle koniske spiraltannhjul og kan betraktes som en hybrid mellom koniske tannhjul og snekkedrift.

Ved store nok spiraltenner vil systemet fungere svært likt som et snekkesystem ved at kronhjulet vil bli låst.

Hypoidtannhjul brukes mye i biler ved kraftoverføring mellom drivaksel og bakaksel.

Koniske spiraltannhjul som har kryssende senterlinjer er ikke hypoidtannhjul.

 

Modul og konstruksjon av tannhjul

I det metriske ISO system standardiseres kalkulering av tannhjul med en verdi som kalles 'modul'. Modulen til et tannhjul representerer størrelsen på tennene. Sammen med tannhjulets diameter og tanntall skaper det det hellige tannhjuls treenighet.

 

Modul er en enkel standard som definerer høyden, bredden og tykkelsen av tenner på et tannhjul basert på gitte parametere. Derav navnet "modul" av latin for 'enhet' eller 'forhold'. Den hellige tannhjuls treenighet sier at hvis du har 2 av 3 verdier kan du finne alt du trenger å vite om et tannhjul.

Det finnes også de vantro som ikke tror på den hellige Modul men heller vil bruke Diametral Pitch (hovedsaklig USA).

Modul og DP uttrykker det samme, men på motsatt måte, som man kan se i tabellen over.

Modul måler hvor hvor mange millimeter som går til hver tann.

Diametral pitch måler hvor mange tenner som går på en tomme.

Her ser man forholdet mellom Modul (over) og DP (under). Et høyere tall i Modulsystemet gir større tenner fordi det fordeler én tann over en større del av tannhjulet, men mindre tenner i DP-systemet siden det representerer flere tenner fordelt på den samme avstanden.

Begge systemer ender opp i 0,5 eller andre mindre-enn-én desimaltall, men på forskjellig ende av skalaen. 0,5 Modul betyr en veldig liten tann, mens 0,5 DP betyr en stor tann på to tommer.

For å konvertere mellom systemene kan følgende formler brukes:

 

Men for å virkelig forstå de hellige skrifter må vi først foreta en liten introduksjon til tannhjulets anatomi:

Det finnes mange rare og vanskapte tannhjul som ikke lar seg definere med modul, de går rundt, men disse vil ende opp i tannhjul-helvete når de kastes der alt er firkantet.

Delesirkelen er den interessante sirkelen her. Det er den vi kalkulerer alle de andre målene etter. Den går gjennom midten av tennene og representerer kontaktpunktet med det andre tannhjulet.

Tannhjul i inngrep møtes ved delesirkelen.

Tannhjul i inngrep må ha samme modul!

Senteravstanden mellom tannhjulene er summen av delesirkeldiameterne delt på to.

Så hvordan er dette magiske forholdet som modulen definerer?

Ved å bruke modul som en standard proporsjon kan vi kalkulere og produsere pålitelige tannhjul.

Hvis vi har en gitt utveksling som skal oppnås, d.v.s. vi vet tanntallet, og vi vet modulen kan vi kalkulere hvor stort tannhjulet blir og deretter alle de andre målene vi trenger.

Hvis vi har en gitt størrelse og tanntall kan vi finne ut hva modulen må være for å få et korrekt og velfungerende tannhjul.

Hvis vi vet modulen og størrelsen kan vi kalkulere tanntallet.

Delingen er avstanden mellom tennene målt fra to like punkter på hver tann på delesirkelen som den får sitt navn fra.

Delingen kalkuleres slik:

I land som bruker diametrisk deling (Diametral Pitch (DP)) bruker de også tommer og Circular Pitch (CP) finnes ved å erstatte Modul med DP i formelen over.

 

Her står m for modul, ikke meter...

Andre kjekke formler:

Toppsirkeldiameteren da = (Z+2)m fordi da = z*m + 2*m siden den er èn ganger modulen lenger ut på begge sider, derav +2 o.s.v.

Etc...  Flere andre formler kan ekstrapoleres via det som er gitt, over er bare noen eksempler.

 

Ved kalkulering av sylindriske tannhjul med heliske tenner er det to måter å produsere de på. Enten ved å bruke 'Pn' som er "pitch normal" eller 'Pt' som er "pitch transverse". Pt er den transverse delingen, det vil si sett radialt på hjulet (ovenfra). Pn er den normale delingen sett fra siden. Siden tennene er skrå er den transverse modulen Mt lenger enn den normale Mn som gjør at man må endre verktøyet etter heliksvinkelen dersom man skjærer tannhjul med det transverse system, men med det normale system kan man bruke det samme verktøyet uavhengig av heliksvinkelen.

 

Ved kalkulering av koniske tannhjul er det vinklene som definerer tennene, ikke diameteren.

Det finnes også koniske tannhjul med ikke-vinklede tenner. I disse tilfellene brukes diameterne istedenfor vinklene for kalkulering.

 

Når det kommer til snekkesystemer er det tre forhold å ta hensyn til, aksial modul, normal modul og transvers modul.

Her sett fra den aksiale vinkel.

Px er den aksiale delingen, Pn den normale og Pt den transverse.

β er stigningsvinkelen og er den samme som snekkehjulets heliksvinkel.

 

Pressvinkelen er en faktor som bidrar til å bestemme tannprofilen. Før var det vanlig med en pressvinkel på 14,5 grader, men i dag er det mer vanlig med 20 grader spesielt i evolventfortanning. Evolventfortanning er tenner med en profil som sørger for konstant kontakt mellom tannhjulene og jevn overføring av kraft.

Tannhjul har fasetterte tenner for at tennene skal gå klar av hverandre. Hadde tennene vært helt firkantet ville de låst seg.

Evolventen av en sirkel er kurven som dannes når man vikler en imaginær tråd stramt av sirkelen.

Det er altså en del av omkretsen dratt ut fra et punkt på sirkelen til tangenten til punktet med samme lengde som stykket med omkrets som er viklet av.

Det viser seg at evolvente kurver er ypperlig til bruk i tannhjul. De gir en konstant kontakt og jevn pressvinkel.